如图,已知四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=DC, 点E是PC的中点,作 交PB于点F.
交PB于点F.

(1)求证:PB⊥平面EFD;
(2)求二面角C-PB-D的大小.
设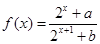 是定义在
是定义在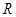 上的奇函数(
上的奇函数( 为实常数).
为实常数).
(1)求 与
与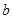 的值;
的值;
(2)证明函数 的单调性并求函数
的单调性并求函数 的值域.
的值域.
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是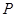 (万元)和
(万元)和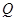 (万元),它们与投入资金
(万元),它们与投入资金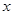 (万元)的关系有经验公式:
(万元)的关系有经验公式: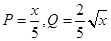 .今有
.今有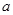 万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点, 是
是 的中点,直线
的中点,直线 与
与 相交于点
相交于点 .
.
(1)求圆 的方程;
的方程;
(2)当 时,求直线
时,求直线 的方程;
的方程;
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.