高中数学解答题

（本小题满分10分）已知全集，若，，求实数、的值．

（本小题满分13分）已知点P（一1，）是椭圆E：上一点F₁，F₂分别是椭圆E的左、右焦点，O是坐标原点，PF₁⊥x轴．
（1）求椭圆E的方程；
（2）设A，B是椭圆E上两个动点，满足：，求直线AB的斜率

已知函数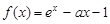（e为自然对数的底数），a＞0．
（1）若函数恰有一个零点，证明：；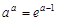
（2）若≥0对任意x∈R恒成立，求实数a的取值集合．

己知圆的参数方程为（为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．
（1）将圆的参数方程他为普通方程，将圆的极坐标方程化为直角坐标方程；
（2）圆，是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．

（本小题满分13分）已知数列满足，为其前项和，且.
（1）求的值；
（2）求证：；
（3）判断数列是否为等差数列，并说明理由.

（本小题满分13分）设数列是首项为，公差为的等差数列，且是等比数列的前三项.
（1）求的通项公式；
（2）求数列的前项和.

，求

设△ABC的内角 的对边分别为 且 
（Ⅰ）求角A的值；
（Ⅱ）当角A钝角时，求BC边上的高.

求经过直线的交点且平行于直线的直线方程

已知数列是等比数列，且，，．
（1）求数列的通项公式；
（2）如数列的前项和为，求．

已知函数，是常数．
（1）求函数的图象在点处的切线的方程；
（2）证明函数的图象在直线的下方；
（3）讨论函数零点的个数．

已知命题：函数在上单调递增；命题：不等式的解集为，若为真，为假，求实数的取值范围．

已知函数= （A>0，）的图像如图所示.

（1）求，，；
（2）=+，若对任意的，都有，求的取值范围.

某校在一次期末数学统测中，为统计学生的考试情况，从学校的2000名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间（满分150分），将统计结果按如下方式分成八组：第一组，第二组，……，第八组，下图是按上述分组方法得到的频率分布直方图的一部分．

（1）求第七组的频率，并完成频率分布直方图；
（2）估计该校的2000名学生这次考试成绩的平均分(可用中值代替各组数据平均值)；
（3）若从样本成绩属于第六组和第八组的所有学生中随机抽取两名，求他们的分差不小于10分的概率．

已知二次函数，其导函数的零点为，.
（1）若函数在区间上是单调函数，求实数的取值范围；
（2）若函数的图象总在函数图象的上方，求的取值范围．