已知函数 ,其中
,其中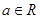 .
.
(1)当 时,求函数
时,求函数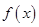 的图象在点
的图象在点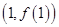 处的切线方程;
处的切线方程;
(2)如果对于任意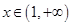 ,都有
,都有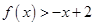 ,求
,求 的取值范围.
的取值范围.
(本小题满分15分)
已知函数 其中e为自然对数的底数。
其中e为自然对数的底数。
(I)若函数f (x)在[1, 2]上为单调增函数,求实数a的取值范围;
(II)设曲线y=" f" (x)在点P(1, f (1))处的切线为l .试问:是否存在正实数a ,使得函数y=" f" (x)的图象被点P 分割成的两部分(除点P 外)完全位于切线l 的两侧?若存在,请求出a 满足的条件,若不存在,请说明理由.
若曲线 与曲线
与曲线 在它们的公共点
在它们的公共点 处具有公共切线,则实数
处具有公共切线,则实数 ( )
( )
A. |
B. |
C. |
D. |
设函数 f (x)=ax-lnx-3(a∈R),g(x)=xe1-x.
(Ⅰ)若函数 g(x) 的图象在点 (0,0) 处的切线也恰为 f (x) 图象的一条切线,求实数 a的值;
(Ⅱ)是否存在实数a,对任意的 x∈(0,e],都有唯一的 x0∈[e-4,e],使得 f (x0)=g(x) 成立.若存在,求出a的取值范围;若不存在,请说明理由.
注:e是自然对数的底数.
已知函数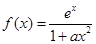 ,其中
,其中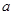 为实数,常数
为实数,常数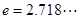 .
.
(1) 若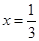 是函数
是函数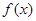 的一个极值点,求
的一个极值点,求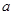 的值;
的值;
(2) 当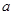 取正实数时,求函数
取正实数时,求函数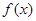 的单调区间;
的单调区间;
(3) 当 时,直接写出函数
时,直接写出函数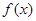 的所有减区间.
的所有减区间.
已知函数 ∈R).
∈R).
(1)若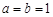 ,求
,求 点(
点(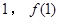 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较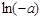 与
与 的大小.
的大小.