设L为曲线C:y= 在点(1,0)处的切线.
在点(1,0)处的切线.
(1)求L的方程;
(2)证明:除切点(1,0)之外,曲线C在直线L的下方.
设函数f(x)= D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
已知函数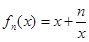 ,(
,(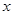 >0,
>0,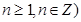 ,以点
,以点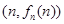 为切点作函数
为切点作函数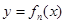 图象的切线
图象的切线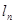 ,记函数
,记函数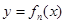 图象与三条直线
图象与三条直线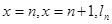 所围成的区域面积为
所围成的区域面积为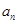 .
.
(1)求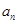 ;
;
(2)求证: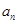 <
<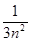 ;
;
(3)设 为数列
为数列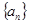 的前
的前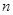 项和,求证:
项和,求证: <
<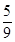 .来
.来
设定义在(0,+∞)上的函数f(x)=ax+ +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y= x,求a,b的值.
x,求a,b的值.
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直线m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
若曲线f(x)=ax2+lnx存在垂直于y轴的切线,则实数a的取值范围是 .
已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.
若曲线y=x- 在点(m,m-
在点(m,m- )处的切线与两坐标轴围成三角形的面积为18,则m=________.
)处的切线与两坐标轴围成三角形的面积为18,则m=________.
直线y= x+b与曲线y=-
x+b与曲线y=- x+ln x相切,则b的值为( )
x+ln x相切,则b的值为( )
| A.-2 | B.1 | C.- |
D.-1 |
设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数为f′(x),且f′(x)是偶函数,则曲线y=f(x)在原点处的切线方程为________.
函数f(x)=2lnx+x2-bx+a(b>0,a∈R)在点(b,f(b))处的切线斜率的最小值是( )
A.2 |
B.2 | C. |
D.1 |
已知函数f(x)=x3+f′ x2-x,f(x)的图像在点
x2-x,f(x)的图像在点 ,f
,f 处的切线的斜率是________.
处的切线的斜率是________.
已知函数f(x)= +xln x,则曲线y=f(x)在x=1处的切线方程为( )
+xln x,则曲线y=f(x)在x=1处的切线方程为( )
| A.x-y-3=0 | B.x-y+3=0 | C.x+y-3=0 | D.x+y+3=0 |