安徽省合肥市高三第一次教学质量检测理科数学试卷
设集合 则“
则“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
过坐标原点O作单位圆 的两条互相垂直的半径
的两条互相垂直的半径 ,若在该圆上存在一点
,若在该圆上存在一点 ,使得
,使得 (
( ),则以下说法正确的是( )
),则以下说法正确的是( )
A.点 一定在单位圆内 一定在单位圆内 |
B.点 一定在单位圆上 一定在单位圆上 |
C.点 一定在单位圆外 一定在单位圆外 |
D.当且仅当 时,点 时,点 在单位圆上 在单位圆上 |
过双曲线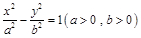 的一个焦点作实轴的垂线,交双曲线于
的一个焦点作实轴的垂线,交双曲线于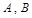 两点,若线段
两点,若线段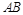 的长度恰等于焦距,则双曲线的离心率为( )
的长度恰等于焦距,则双曲线的离心率为( )
A.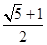 |
B.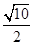 |
C.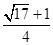 |
D.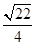 |
在 中,已知
中,已知 ,
, ,则
,则 为( )
为( )
| A.等边三角形 | B.等腰直角三角形 |
| C.锐角非等边三角形 | D.钝角三角形 |
对于函数 ,若
,若 为某一三角形的三边长,则称
为某一三角形的三边长,则称 为“可构造三角形函数”.已知函数
为“可构造三角形函数”.已知函数 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A. |
B. |
C. |
D. |
某办公室共有6人,组织出门旅行,旅行车上的6个座位如图所示,其中甲、乙两人的关系较为亲密,要求在同一排且相邻,则不同的安排方法有 种.
已知直线: (
( 为给定的正常数,
为给定的正常数, 为参数,
为参数, )构成的集合为
)构成的集合为 ,给出下列命题:
,给出下列命题:
①当 时,
时, 中直线的斜率为
中直线的斜率为 ;
;
② 中所有直线均经过一个定点;
中所有直线均经过一个定点;
③当 时,存在某个定点,该定点到
时,存在某个定点,该定点到 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当 时,
时, 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为 ;
;
⑤ 中的所有直线可覆盖整个平面.
中的所有直线可覆盖整个平面.
其中正确的是 (写出所有正确命题的编号).
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB= AB.直角梯形ACEF中,
AB.直角梯形ACEF中, ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.
(1)求证: ;
;
(2)若直线DE与平面ACEF所成的角的正切值是 ,试求
,试求 的余弦值.
的余弦值.
已知函数 在
在 处取得极小值.
处取得极小值.
(1)若函数 的极小值是
的极小值是 ,求
,求 ;
;
(2)若函数 的极小值不小于
的极小值不小于 ,问:是否存在实数
,问:是否存在实数 ,使得函数
,使得函数 在
在 上单调递减?若存在,求出
上单调递减?若存在,求出 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
已知椭圆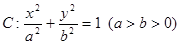 的右焦点为
的右焦点为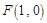 ,设左顶点为A,上顶点为B且
,设左顶点为A,上顶点为B且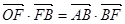 ,如图.
,如图.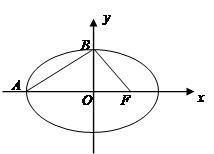
(1)求椭圆 的方程;
的方程;
(2)若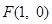 ,过
,过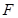 的直线
的直线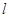 交椭圆于
交椭圆于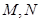 两点,试确定
两点,试确定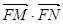 的取值范围.
的取值范围.
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4, ,9;6个国产品牌奶粉的样品编号为10,11,12,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用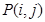 表示编号为
表示编号为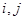
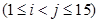 的样品首轮同时被抽到的概率.
的样品首轮同时被抽到的概率.
(1)求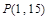 的值;
的值;
(2)求所有的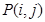
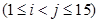 的和.
的和.
 表示复数
表示复数 的共轭复数,则
的共轭复数,则 ( )
( )






 ,则一定在函数
,则一定在函数 图象上的点是( )
图象上的点是( )




 满足
满足 时,
时, 的最大值为1,则
的最大值为1,则 的最小值为( )
的最小值为( ) ,且
,且 ,则
,则 __________.
__________. 满足
满足 且
且 ,则
,则 .
. 展开式的各项系数绝对值之和为1024,则展开式中
展开式的各项系数绝对值之和为1024,则展开式中 项的系数为_____________.
项的系数为_____________. 求:
求: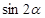 ;
; .
.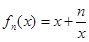 ,(
,(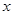 >0,
>0,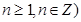 ,以点
,以点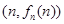 为切点作函数
为切点作函数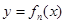 图象的切线
图象的切线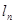 ,记函数
,记函数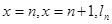 所围成的区域面积为
所围成的区域面积为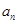 .
.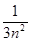 ;
; 为数列
为数列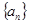 的前
的前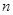 项和,求证:
项和,求证: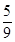 .来
.来 粤公网安备 44130202000953号
粤公网安备 44130202000953号