高考数学全程总复习课时提升作业三十七第六章第三节练习卷
若不等式Ax+By+5<0表示的平面区域不包括点(2,4),且k=A+2B,则k的取值范围是( )
A.k≥- |
B.k≤- |
C.k>- |
D.k<- |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
若不等式组 所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
A. |
B. |
C. |
D.2 |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
已知变量x,y满足约束条件 则目标函数z=3x-y的取值范围是( )
则目标函数z=3x-y的取值范围是( )
A.[- ,6] ,6] |
B.[- ,-1] ,-1] |
| C.[-1,6] | D.[-6, ] ] |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
已知x,y满足条件 则
则 的取值范围是( )
的取值范围是( )
A.[ ,9] ,9] |
B.(-∞, )∪(9,+∞) )∪(9,+∞) |
| C.(0,9) | D.[-9,- ] ] |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
设 =(1,
=(1, ),
), =(0,1),O为坐标原点,动点P(x,y)满足0≤
=(0,1),O为坐标原点,动点P(x,y)满足0≤ ·
· ≤1,0≤
≤1,0≤ ·
· ≤1,则z=y-x的最大值是( )
≤1,则z=y-x的最大值是( )
A. |
B.1 | C.-1 | D.-2 |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
某运输公司有12名驾驶员和19名工人,有8辆载重为10吨的甲型卡车和7辆载重为6吨的乙型卡车.某天需运往A地至少72吨的货物,派用的每辆车需满载且只运送一次,派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z=( )
| A.4650元 | B.4700元 |
| C.4900元 | D.5000元 |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
若实数x,y满足 则x2-2xy+y2的取值范围是( )
则x2-2xy+y2的取值范围是( )
| A.[0,4] | B.[0, ] ] |
C.[4, ] ] |
D.[0, ] ] |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
若x,y满足约束条件 且目标函数z=ax+by(a>0,b>0)的最大值为7,则
且目标函数z=ax+by(a>0,b>0)的最大值为7,则 +
+ 的最小值为( )
的最小值为( )
| A.14 | B.7 | C.18 | D.13 |
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
函数f(x)=x3+bx2+cx+d在区间[-2,2]上是减函数,则b+c的最大值为 .
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
已知点P(2,t)在不等式组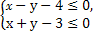 表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为 .
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷
设函数f(x)= D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷

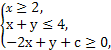 且目标函数z=3x+y的最小值是5,则z的最大值是 .
且目标函数z=3x+y的最小值是5,则z的最大值是 .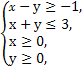 则z=x-2y的取值范围为 .
则z=x-2y的取值范围为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号