若曲线y=x2+ax+b在点(0,b)处的切线方程是x y+1=0,则( )
y+1=0,则( )
A.a= 1,b=1 1,b=1 |
B.a= 1,b= 1,b= 1 1 |
C.a=1,b= 1 1 |
D.a=1,b=1 |
定义在R上的函数 ,满足
,满足 ,若
,若 且
且 ,则有( )
,则有( )
A. |
B. |
C. |
D.不能确定 |
设函数f(x)= ax3+
ax3+ bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.
bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.
已知函数 ,在定义域
,在定义域 上表示的曲线过原点,且在
上表示的曲线过原点,且在 处的切线斜率均为
处的切线斜率均为 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 ; ④若对
; ④若对 ,
, 恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为
若存在实常数 和
和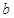 ,使得函数
,使得函数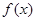 和
和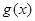 对其定义域上的任意实数
对其定义域上的任意实数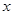 分别满足:
分别满足: 和
和 ,则称直线
,则称直线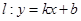 为
为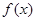 和
和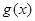 的“隔离直线”.已知函数
的“隔离直线”.已知函数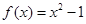 和函数
和函数 ,那么函数
,那么函数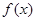 和函数
和函数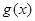 的隔离直线方程为_________.
的隔离直线方程为_________.
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求f(x)的单调区间.
已知函数 ,
, ,函数
,函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定 与
与 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意 ,都有
,都有 成立。
成立。
已知函数f(x)=xlnx,过点A  作函数y=f(x)图象的切线,则切线的方程为________.
作函数y=f(x)图象的切线,则切线的方程为________.