北京市石景山区高三一模文科数学试卷
在等比数列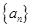 中,
中,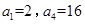 ,则数列
,则数列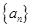 的通项公式
的通项公式 _____________,设
_____________,设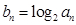 ,则数列
,则数列 的前
的前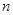 项和
项和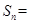 _____________.
_____________.
来源:2014届北京市石景山区高三一模文科数学试卷
一艘轮船在匀速行驶过程中每小时的燃料费与它速度的平方成正比,除燃料费外其它费用为每小时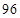 元. 当速度为
元. 当速度为 海里/小时时,每小时的燃料费是
海里/小时时,每小时的燃料费是 元. 若匀速行驶
元. 若匀速行驶 海里,当这艘轮船的速度为___________海里/小时时,费用总和最小.
海里,当这艘轮船的速度为___________海里/小时时,费用总和最小.
来源:2014届北京市石景山区高三一模文科数学试卷
若存在实常数 和
和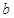 ,使得函数
,使得函数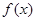 和
和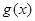 对其定义域上的任意实数
对其定义域上的任意实数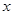 分别满足:
分别满足: 和
和 ,则称直线
,则称直线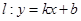 为
为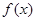 和
和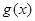 的“隔离直线”.已知函数
的“隔离直线”.已知函数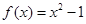 和函数
和函数 ,那么函数
,那么函数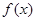 和函数
和函数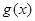 的隔离直线方程为_________.
的隔离直线方程为_________.
来源:2014届北京市石景山区高三一模文科数学试卷
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在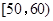 的频率及全班人数;
的频率及全班人数;
(2)求分数在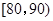 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中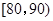 间矩形的高;
间矩形的高;
(3)若要从分数在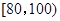 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在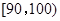 之间的概率.
之间的概率.
来源:2014届北京市石景山区高三一模文科数学试卷
如图,已知四棱锥 ,
, ,
, ,
, 平面
平面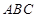 ,
,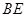 ∥
∥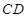 ,
, 为
为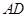 的中点.
的中点.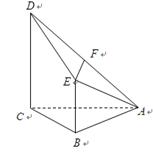
(1)求证: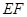 ∥平面
∥平面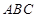 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求四棱锥 的体积.
的体积.
来源:2014届北京市石景山区高三一模文科数学试卷
已知函数 .
.
(1)若 在
在 处取得极值,求实数
处取得极值,求实数 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)若 在
在 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围.
来源:2014届北京市石景山区高三一模文科数学试卷
给定椭圆 :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“准圆”.若椭圆
的“准圆”.若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点 是椭圆
是椭圆 的“准圆”上的动点,过点
的“准圆”上的动点,过点 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段 的长为定值.
的长为定值.
来源:2014届北京市石景山区高三一模文科数学试卷
 ,集合
,集合 ,
, ,那么
,那么 ( )
( )



 内单调递减,并且是偶函数的是( )
内单调递减,并且是偶函数的是( )



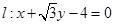 与圆
与圆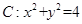 的位置关系是( )
的位置关系是( )
 的渐近线方程是
的渐近线方程是 ,则其离心率为( )
,则其离心率为( )
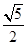


 且图象关于直线
且图象关于直线 对称的函数是( )
对称的函数是( )
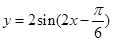
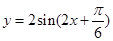


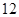
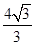


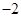


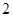
 在椭圆
在椭圆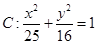 上,
上, 为椭圆
为椭圆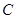 的右焦点,若点
的右焦点,若点 满足
满足 且
且 ,则
,则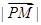 的最小值为( )
的最小值为( )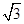
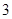
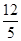
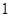
 是虚数单位,计算
是虚数单位,计算 _________.
_________.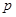 :
: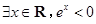 ,则
,则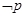 是____________________.
是____________________. 满足约束条件
满足约束条件 则
则 的最大值是_________.
的最大值是_________.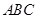 中,角
中,角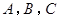 的对边分别为
的对边分别为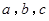 ,且
,且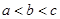 ,
,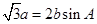 .
.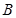 的大小;
的大小; ,
, ,求
,求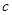 边的长和△
边的长和△ ,把
,把 作为新数列
作为新数列 的第一项,把
的第一项,把 或
或 (
( )作为新数列
)作为新数列 项,数列
项,数列 的一个生成数列是
的一个生成数列是 .已知数列
.已知数列 的生成数列,
的生成数列, 为数列
为数列 项和.
项和. 的所有可能值;
的所有可能值; ,求
,求 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号