已知某四棱锥的三视图(单位:cm)如图所示,则该四棱锥的体积是 ()
A. |
B. |
C. |
D. |
—个几何体的三视图及其尺寸如图所示,则该几何体的表面积为()
A. |
B. |
C. |
D. |
如图所示,矩形ABDE中,AB=3,BD=6, ,又在
,又在 中,点F为BC的中点,且
中,点F为BC的中点,且

(1)求证: ;
;
(2)求证: ;
;
(3)求三棱锥A—CDE的体积V。
如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,A1A=AB=2,BC=3.
(Ⅰ)求证:AB1∥平面BC1D;
(Ⅱ)求四棱锥B﹣AA1C1D的体积.
(本小题满分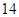 分)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,
分)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,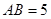 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.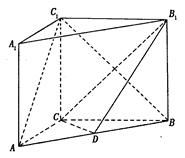
(1)求证:AC⊥BC1;
(2)求多面体 的体积;
的体积;
(3)求二面角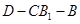 的平面角的正切值.
的平面角的正切值.
如图,正方体ABCD—A1B1C1D1,
则下列四个命题:
①P在直线BC1上运动时,三棱锥A—D1PC的体积不变;
②P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
③P在直线BC1上运动时,二面角P—AD1—C的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是过D1点的直线D1A1.
其中真命题的编号是 .
(本小题满分12分)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
(本小题满分12分)如图,在直三棱柱 中,
中, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分14分)如图几何体中,四边形 为矩形,
为矩形, ,
, ,
, ,
, ,
, 为
为 的中点,
的中点, 为线段
为线段 上的一点,且
上的一点,且 .
.
(1)证明: 平面
平面 ;
;
(2)证明:平面 平面
平面 ;
;
(3)求三棱锥 的体积
的体积 .
.
(本小题满分14分)如图,直三棱柱 中,
中, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)证明: 平面
平面 ;
;
(2)设 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分14分)如图,在四棱锥S-ABCD中,底面ABCD为菱形, ,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
(1)求证:PQ∥平面SAD;
(2)求证:AC⊥平面SEQ;
(3)如果SA=AB=2,求三棱锥S-ABC的体积.
【原创】(本小题满分12分)如图,在三棱锥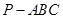 中,
中,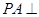 底面ABC,
底面ABC, ,AP=AC, 点
,AP=AC, 点 ,
,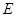 分别在棱
分别在棱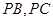 上,且BC//平面ADE.
上,且BC//平面ADE.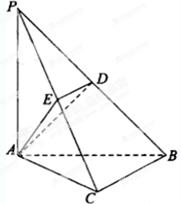
(Ⅰ)求证:DE⊥平面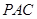 ;
;
(Ⅱ)若PC⊥AD,且三棱锥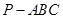 的体积为8,求多面体ABCED的体积.
的体积为8,求多面体ABCED的体积.