高中数学表面展开图试题

某几何体的三视图如图示，则此几何体的体积是（）

A．

B．

C．

D．

已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，则此球的表面积等于__________．

已知某几何体的三视图如图所示，则该几何体的体积等于（）

A．	B．160
C．	D．60

已知三棱锥,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥的体积为,则球的表面积是（）

A．

B．

C．

D．

已知四棱锥，其中，，面，，为的中点．

（1）求证：面；
（2）求证：面面；
（3）求四棱锥的体积．

如图，已知正方形和矩形所在的平面互相垂直，，，是线段的中点．

（1）求三棱锥的体积；
（2）求与平面所成的角大小．

如图，在四棱锥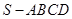中，底面ABCD是菱形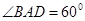，，侧面底面ABCD，并且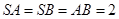，F为SD的中点.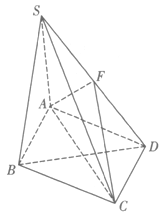

（1）求三棱锥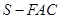的体积；
（2）求直线BD与平面FAC所成角的正弦值.

利用一个球体毛坯切削后得到一个四棱锥,其中底面四边形是边长为的正方形，，且平面,则球体毛坯体积的最小值应为 ．

已知的三边长分别为，，，是边上的点，是平面外一点．给出下列四个命题：
①若平面，且是边中点，则有；
②若，平面，则面积的最小值为；
③若，平面，则三棱锥的外接球体积为；
④若，在平面上的射影是内切圆的圆心，则三棱锥的体积为；
其中正确命题的序号是 （把你认为正确命题的序号都填上）．

所谓正三棱锥，指的是底面为正三角形，顶点在底面上的射影为底面三角形中心的三棱锥，在正三棱锥中，是的中点，且，底面边长，则正三棱锥的体积为 ，其外接球的表面积为 ．

如图：已知四棱柱的底面是菱形，该菱形的边长为1，，．

（1）设棱形的对角线的交点为，求证：//平面；
（2）若四棱柱的体积，求与平面所成角的正弦值．

如图，边长为2的正方形绕边所在直线旋转一定的角度（小于）到的位置．

（1）若，求三棱锥的外接球的表面积；
（2）若为线段上异于，的点，，设直线与平面所成角为，当时，求的取值范围．

如图，在三棱柱中，侧棱垂直于底面，，，，，分别是，的中点．

（1）求证：平面平面；
（2）求证：平面；
（3）求三棱锥的体积．

如图，在多面体中，已知是边长为1的正方形，且，均为正三角形，，，则多面体的体积为（）

A．

B．

C．

D．

如图，在三棱柱中，侧棱垂直于底面，，，、分别为、的中点．

（1）求证：平面平面；
（2）求证：平面；
（3）求三棱锥的体积．