以下四个关于圆锥曲线的命题中:
①双曲线 与椭圆
与椭圆 有相同的焦点;
有相同的焦点;
②在平面内, 设 、
、 为两个定点,
为两个定点, 为动点,且
为动点,且 ,其中常数
,其中常数 为正实数,则动点
为正实数,则动点 的轨迹为椭圆;
的轨迹为椭圆;
③方程 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④过双曲线 的右焦点
的右焦点 作直线
作直线 交双曲线于
交双曲线于 两点,若
两点,若 ,则这样的直线
,则这样的直线 有且仅有3条。
有且仅有3条。
其中真命题的序号为 (写出所有真命题的序号).
下列有关命题的说法:
①命题“若 ,则
,则 ”的逆否命题为真命题;
”的逆否命题为真命题;
②“ ”是“直线
”是“直线 相互垂直”的充要条件;
相互垂直”的充要条件;
③已知命题 对任意的
对任意的
 .若命题
.若命题 是假命题,则实数
是假命题,则实数 的取值范围是
的取值范围是 ;
;
④“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为 ”的充分不必要条件。
”的充分不必要条件。
其中正确的有 。
给出下列命题:
① ;
;
②函数y=sin(2x+ )的图像关于点
)的图像关于点 对称;
对称;
③将函数y=cos(2x- )的图像向左平移
)的图像向左平移  个单位,可得到函数y=cos2x的图像;
个单位,可得到函数y=cos2x的图像;
④函数 的最小正周期是
的最小正周期是 .
.
其中正确的命题的序号是 .
有下列叙述
①集合
②两向量平行,那么两向量的方向一定相同或者相反
③若不等式 对任意正整数
对任意正整数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
④对于任意两个正整数 ,
, ,定义某种运算
,定义某种运算 如下:
如下:
当 ,
, 奇偶性相同时,
奇偶性相同时, 

 =
= ;当
;当 ,
, 奇偶性不同时,
奇偶性不同时,

 =
= ,在此定义下,集合
,在此定义下,集合 .
.
上述说法正确的是____________
给出下列命题:
①函数 与函数
与函数 的图象关于
的图象关于 对称
对称
②函数 导函数为
导函数为 ,若
,若 ,则
,则 必为函数
必为函数 的极值.
的极值.
③函数 在一象限单调递增
在一象限单调递增
④ 在其定义域内为单调增函数.
在其定义域内为单调增函数.
其中正确的命题序号为
给出下列命题:
①半径为2,圆心角的弧度数为 的扇形面积为
的扇形面积为 ;
;
②若 、
、 为锐角,
为锐角, 则
则 ;
;
③函数 的一条对称轴是
的一条对称轴是 ;
;
④ 是函数
是函数 为偶函数的一个充分不必要条件.
为偶函数的一个充分不必要条件.
其中真命题的序号是 .
给出以下五个命题:
① ,若
,若 ,则
,则 或
或 的否命题是假命题;
的否命题是假命题;
②函数 的最小值为2;
的最小值为2;
③若函数 的图象关于点(1,0)对称,则
的图象关于点(1,0)对称,则 的值为-3;
的值为-3;
④若 ,则函数
,则函数 是以4为周期的周期函数;
是以4为周期的周期函数;
⑤若(1+x)10 =a0+a1x+a2x2 +… +a10x10,则a0+a1 +2a2+3a3 +… +10a10=10×29.
其中真命题的序号是___________.
定义:在数列 中,若
中,若 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列 是等差数列;②
是等差数列;② 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列 (k∈N*,k为常数)也是“等方差数列”;
(k∈N*,k为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
已知下列结论:
①已知 为实数,则“
为实数,则“ ”是“
”是“ 成等比数列”的充要条件;
成等比数列”的充要条件;
②满足条件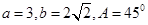 的△ABC的个数为2;
的△ABC的个数为2;
③若两向量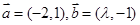 的夹角为钝角,则实数
的夹角为钝角,则实数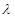 的取值范围
的取值范围
为 ;
;
④若 为三角形中的最小内角,则函数
为三角形中的最小内角,则函数 的值域是
的值域是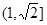 ;
;
⑤某厂去年12月份产值是同年一月份产值的m倍,则该厂去年的月平均增长率
为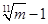 ;
;
则其中正确结论的序号是__________;
①若 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数, ,则
,则 ;
;
②若锐角 、
、 满足
满足 则
则 ;
;
③在 中,“
中,“ ”是“
”是“ ”成立的充要条件;
”成立的充要条件;
④要得到函数 的图象,只需将
的图象,只需将 的图象向右平移
的图象向右平移 个单位。
个单位。
其中是真命题的有 (填写正确命题题号)
已知定义域为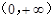 的函数
的函数 满足:①对任意
满足:①对任意 ,恒有
,恒有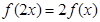 成立;当
成立;当 时,
时,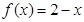 。给出如下结论:
。给出如下结论:
①对任意 ,有
,有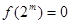 ;②函数
;②函数 的值域为
的值域为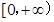 ;③存在
;③存在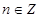 ,使得
,使得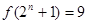 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在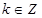 ,使得
,使得 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.