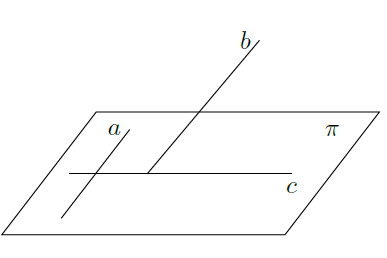
(1)如图,证明命题"a是平面
内的一条直线,b是
外的一条直线(b不垂直于
),c是直线b在
上的投影,若
,则
"为真。
(2)写出上述命题的逆命题,并判断其真假(不需要证明)
已知函数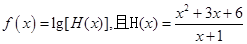 ,
,
(1)求函数 的定义域;
的定义域;
(2)求函数 在区间
在区间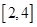 上的最小值;
上的最小值;
(3)已知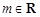 ,命题p:关于x的不等式
,命题p:关于x的不等式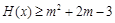 对函数
对函数 的定义域上的任意
的定义域上的任意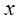 恒成立;命题q:指数函数
恒成立;命题q:指数函数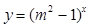 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
已知 ,设p:函数
,设p:函数 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
q:曲线y=x2+(2a 3)x+1与x轴交于不同的两点.若“p且q”为假,“﹁q”为假,求a的取值范围.
已知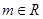 ,命题
,命题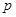 :对任意
:对任意 ,不等式
,不等式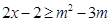 恒成立;命题
恒成立;命题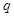 :存在
:存在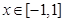 ,使得
,使得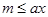 成立
成立
(Ⅰ)若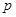 为真命题,求
为真命题,求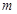 的取值范围;
的取值范围;
(Ⅱ)当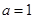 ,若
,若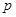 且
且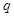 为假,
为假,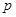 或
或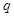 为真,求
为真,求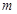 的取值范围。
的取值范围。
(Ⅲ)若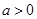 且
且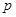 是
是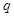 的充分不必要条件,求
的充分不必要条件,求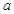 的取值范围。
的取值范围。
设命题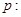 “对任意的
“对任意的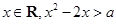 ”,命题
”,命题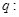 “存在
“存在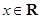 ,使
,使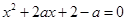 ”.如果命题
”.如果命题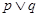 为真,命题
为真,命题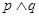 为假,求实数
为假,求实数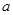 的取值范围.
的取值范围.
设命题p:关于x的不等式2|x-2|<a的解集为;命题q:函数y=lg(ax2-x+a)的值域是R.如果命题p和q有且仅有一个正确,求实数a的取值范围.