高中数学三面角、直三面角的基本性质解答题

已知二次函数的图象过点，其导函数为，数列
的前项和为，点在函数的图象上．
（Ⅰ）求函数的解析式；
（Ⅱ）求数列的通项公式；
（Ⅲ）设，求数列的前项和．

设函数,.    
（Ⅰ）当时，在上恒成立，求实数的取值范围;
（Ⅱ）当时，若函数在上恰有两个不同零点，求实数 的取值范围;
（Ⅲ）是否存在实数，使函数和函数在公共定义域上具有相同的单调性？若存在，求出的值，若不存在，说明理由。

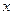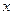某商店以6元/千克的价格购进某种干果1140千克，并对其进行筛选分成甲级干果与乙级干果后同时开始销售。这批干果销售结束后，店主从销售统计中发出：甲级干果与乙级干果在销售过程中每天都有销量，且在同一天卖完；甲级干果从开始销售至销售的第天的总销量（千克）与的关系为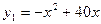；乙级干果从开始销售至销售的第天的总销量（千克）与的关系为，且乙级干果的前三天的销售量的情况见下表：

（1）求、的值；
（2）若甲级干果与乙级干果分别以8元/千克的6元/千克的零售价出售，则卖完这批干果获得的毛利润是多少元？
（3）问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克？
（说明：毛利润=销售总金额-进货总金额。这批干果进货至卖完的过程中的损耗忽略不计）

（1）已知，求的值。
（2）已知是方程的一个根，试求的值。

（本小题满分12分）
某小区要建一个面积为500平方米的矩形绿地，四周有小路，绿地长边外路宽5米，短边外路宽9米，怎样设计绿地的长与宽，使绿地和小路所占的总面积最小，并求出最小值.

 

 

（本小题满分12分）已知函数满足，对任意恒成立，在数列中，对任意
（1）      求函数的解析式
（2）  求数列的通项公式
（3）  若对任意的实数，总存在自然数k，当时，恒成立，求k的最小值。

已知函数其中.
（I）若曲线在处的切线与直线平行，求的值；
（II）求函数在区间上的最小值

二次函数满足。
（1）求函数的解析式；
（2）在区间上，的图象恒在的图象上方，试确定实数的取值范围。

二次函数满足。
（1）求函数的解析式；
（2）在区间上，的图象恒在的图象上方，试确定实数的取值范围。

已知函数．
（1）若从集合中任取一个元素，从集合中任取一个元素，求方程有两个不相等实根的概率；
（2）若是从区间中任取的一个数，是从区间中任取的一个数，求方程没有实根的概率．

（本小题满分12分）已知某种稀有矿石的价值（单位：元）与其重量（单位：克）的平方成正比，且克该种矿石的价值为元。
⑴写出（单位：元）关于（单位：克）的函数关系式；
⑵若把一块该种矿石切割成重量比为的两块矿石，求价值损失的百分率；
⑶把一块该种矿石切割成两块矿石时，切割的重量比为多少时，价值损失的百分率最大。（注：价值损失的百分率；在切割过程中的重量损耗忽略不计）

某单位欲用木料制作如下图所示的框架，框架的下部是边长分别为（单位为：）的矩形，上部是等腰直角三角形，要求框架围成的总面积为，问：分别是多少（精确到）时用料最省？

已知函数．
（1）解关于的不等式；
（2）若对，恒成立，求的取值范围．

已知函数．
（1）若从集合中任取一个元素，从集合中任取一个元素，求方程有两个不相等实根的概率；
（2）若是从区间中任取的一个数，是从区间中任取的一个数，求方程没有实根的概率．

已知．
（1）证明：函数在上为增函数；
（2）用反证法证明：方程没有负数根。