（本小题满分12分）已知函数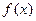
满足
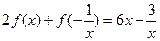，对任意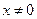
恒成立，在数列
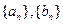中，
对任意
（1） 求函数的解析式
（2） 求数列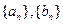的通项公式
（3） 若对任意的实数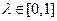
，总存在自然数k，当
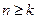时，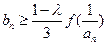
恒成立，求k的最小值。
相关试题
，B=
，C=
，全集为实数集R.
RA)∩B；(2) 如果A∩C≠
，求a的取值范围.
的定义域;(6分)
在
上的值域.
在映射
的作用下的像是
，求
在
在
,
.
的表达式；
和函数
的图象关于原点对称，
在区间
上是增函数，求实数l的取值范围.
顶点的分别为
，其中
．
，求
的值；
，求相关知识点
推荐套卷
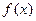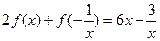（本小题满分12分）已知函数满足，对任意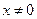恒成立，在数列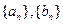中，对任意
（1） 求函数的解析式
（2） 求数列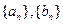的通项公式
（3） 若对任意的实数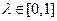，总存在自然数k，当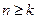时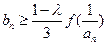，恒成立，求k的最小值。
粤公网安备 44130202000953号