已知函数
．
（1）若从集合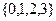
中任取一个元素
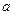，从集合
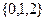中任取一个元素
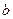，求方程
有两个不相等实根的概率；
（2）若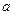是从区间
中任取的一个数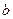，是从区间
中任取的一个数，求方程没有实根的概率．
相关试题
是定义在R上的奇函数，对任意实数
有
成立．
是周期函数，并指出其周期；
，求
的值；
，且
是偶函数，求实数
的值．
，在区间
上有最大值5，最小
上单调，求
的取值范围。
与
都是边长为
的正方形
，点E是
的中点，
平面BDE；
⊥平面BDE
与
的比值。 
，集合
，
；（Ⅱ）若
，试确定实数
的取值范围.
, 
,记函数
已知
的周期为π.
之值;
,试求f(x)的值域.相关知识点
推荐套卷
已知函数．
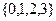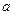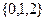（1）若从集合中任取一个元素，从集合中任取一个元素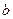，求方程有两个不相等实根的概率；
（2）若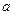是从区间中任取的一个数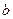，是从区间中任取的一个数，求方程没有实根的概率．
粤公网安备 44130202000953号