(本题共2小题,满分14分。第1小题满分6分,第2小题满分8分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 千米/小时;当车流密度不超过
千米/小时;当车流密度不超过 辆/千米时,车流速度为
辆/千米时,车流速度为 千米/小时,研究表明;当
千米/小时,研究表明;当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)求函数 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
我国加入WTO时,据达成的协议,若干年内某产品关税与市场供应量 的关系允许近似满足
的关系允许近似满足 (其中,
(其中, 为关税的税率,且
为关税的税率,且 ,
, 为市场价格,
为市场价格, 、
、 为正常数),当
为正常数),当 时,市场供应量曲线如图:
时,市场供应量曲线如图:
⑴根据图象求 的值;
的值;
⑵记市场需求量为 ,它近似满足
,它近似满足 ,当
,当 时,市场价格称为市场平衡价格,当市场平衡价
时,市场价格称为市场平衡价格,当市场平衡价 时,求税率的最小值。
时,求税率的最小值。
本题共有3个小题,第1小题满分5分,第2小题满分6分,
第3小题满分7分.
对定义在区间 上的函数
上的函数 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意的
,使得对任意的 都有
都有 ,且对任意的
,且对任意的 都有
都有 恒成立,则称函数
恒成立,则称函数 为区间
为区间 上的“U型”函数。
上的“U型”函数。
(1)求证:函数 是
是 上的“U型”函数;
上的“U型”函数;
(2)设 是(1)中的“U型”函数,若不等式
是(1)中的“U型”函数,若不等式 对一切的
对一切的 恒成立,
恒成立,
求实数 的取值范围;
的取值范围;
(3)若函数 是区间
是区间 上的“U型”函数,求实数
上的“U型”函数,求实数 和
和 的值.
的值.
(本小题满分12分)设函数 ,
, (
( 且
且 )。
)。
(1)设 ,判断
,判断 的奇偶性并证明;
的奇偶性并证明;
(2)若关于 的方程
的方程 有两个不等实根,求实数
有两个不等实根,求实数 的范围;
的范围;
(3)若 且在
且在 时,
时, 恒成立,求实数
恒成立,求实数 的范围。
的范围。
.(本小题满分12分)
已知函数 是定义在实数集R上的奇函数,当
是定义在实数集R上的奇函数,当 >0时,
>0时,
(1)已知函数 的解析式;
的解析式;
(2)若 函数
函数 在区间
在区间 上是单调减函数,求a的取值范围;
上是单调减函数,求a的取值范围;
(3)试证明对 .
.
(本小题满分12分)
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水池的长和宽,使总造价最低.
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000 ,四周空白的宽度为10
,四周空白的宽度为10 ,两栏之间的中缝空白的宽度为5
,两栏之间的中缝空白的宽度为5 ,怎样确定广告的高与宽的尺寸(单位:
,怎样确定广告的高与宽的尺寸(单位: ),能使矩形广告面积最小?
),能使矩形广告面积最小?
(本小题满分12分)
某单位建造一间地面面积为12 平方米的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过 米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
(本小题满分14分)已知函数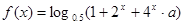 ;
;
(1)若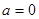 ,求
,求 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断 的单调性;(3)当
的单调性;(3)当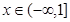 时
时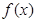 有意义求实
有意义求实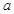 的范围。
的范围。
(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R , ,OB与OM之间的夹角为
,OB与OM之间的夹角为 .
.
(1)将图书馆底面矩形ABCD的面积S表示成 的函数.
的函数.
(2)若 R=45 m,求当 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?
已知二次函数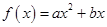 (
(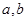 是常数,且
是常数,且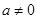 )满足条件:
)满足条件: ,且方程
,且方程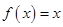 有两个相等实根.
有两个相等实根.
(1)求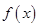 的解析式;
的解析式;
(2)是否存在实数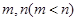 ,使
,使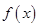 的定义域和值域分别为
的定义域和值域分别为 和
和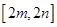 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分14分)
在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,
(1) 建立y与x的函数关系式,并指出其定义域.
(2) 求y的最小值,并指出x的值.