(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R ,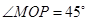 ,OB与OM之间的夹角为
,OB与OM之间的夹角为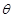 .
.
(1)将图书馆底面矩形ABCD的面积S表示成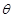 的函数.
的函数.
(2)若 R=45 m,求当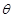 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?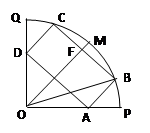
相关知识点
推荐套卷
 中,四边形
中,四边形 为菱形,
为菱形, ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.
 面
面 ;
; 的余弦值;
的余弦值;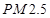 是指大气中直径小于或等于
是指大气中直径小于或等于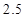 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在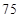 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).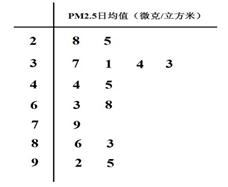
 天数据,记
天数据,记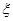 表示抽到
表示抽到 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级. ,
, .
. 的值;
的值; 时,求
时,求 的最值.
的最值.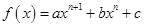
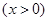 ,其中
,其中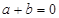 ,
, 为正整数,
为正整数,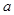 、
、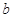 、
、 均为常数,曲线
均为常数,曲线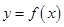 在
在 处的切线方程为
处的切线方程为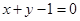 .
. 的最大值;
的最大值;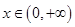 都有
都有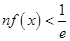 .(
.(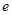 为自然对数的底)
为自然对数的底)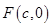 是椭圆
是椭圆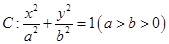 的右焦点;圆
的右焦点;圆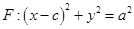 与
与 轴交于
轴交于 两点,其中
两点,其中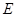 是椭圆
是椭圆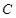 的左焦点.
的左焦点.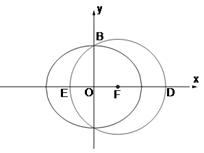
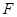 与
与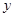 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点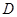 关于
关于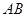 与圆
与圆 与圆
与圆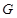 ,若
,若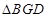 的面积为
的面积为 ,求椭圆
,求椭圆 粤公网安备 44130202000953号
粤公网安备 44130202000953号