如图,已知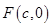 是椭圆
是椭圆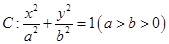 的右焦点;圆
的右焦点;圆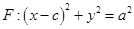 与
与 轴交于
轴交于 两点,其中
两点,其中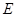 是椭圆
是椭圆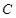 的左焦点.
的左焦点.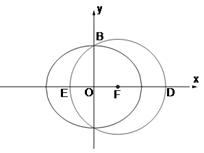
(1)求椭圆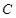 的离心率;
的离心率;
(2)设圆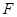 与
与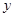 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点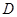 关于
关于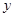 轴的对称点,试判断直线
轴的对称点,试判断直线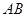 与圆
与圆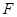 的位置关系;
的位置关系;
(3)设直线 与圆
与圆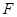 交于另一点
交于另一点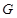 ,若
,若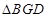 的面积为
的面积为 ,求椭圆
,求椭圆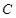 的标准方程.
的标准方程.
推荐套卷
如图,已知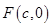 是椭圆
是椭圆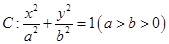 的右焦点;圆
的右焦点;圆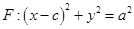 与
与 轴交于
轴交于 两点,其中
两点,其中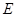 是椭圆
是椭圆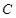 的左焦点.
的左焦点.
(1)求椭圆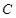 的离心率;
的离心率;
(2)设圆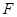 与
与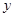 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点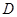 关于
关于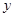 轴的对称点,试判断直线
轴的对称点,试判断直线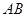 与圆
与圆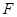 的位置关系;
的位置关系;
(3)设直线 与圆
与圆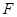 交于另一点
交于另一点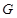 ,若
,若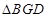 的面积为
的面积为 ,求椭圆
,求椭圆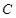 的标准方程.
的标准方程.