关于函数 ,看下面四个结论:
,看下面四个结论:
① 是奇函数;
是奇函数;
②当 时,
时, 恒成立;
恒成立;
③ 的最大值是
的最大值是 ;
;
④ 的最小值是
的最小值是 .
.
其中正确结论的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)将 的图象向左平移
的图象向左平移 个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到
个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到 的图象;若函数
的图象;若函数 在区间
在区间 上的图象与直线
上的图象与直线 有三个交点,求实数a的取值范围.
有三个交点,求实数a的取值范围.
要得到函数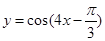 的图象,只需要将函数
的图象,只需要将函数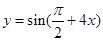 的图象( )
的图象( )
A.向左平移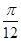 个单位 个单位 |
B.向右平移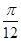 个单位 个单位 |
C.向左平移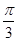 个单位 个单位 |
D.向右平移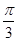 个单位 个单位 |
给出下列五个命题:
①函数 的一条对称轴是
的一条对称轴是 ;
;
②函数 的图象关于点(
的图象关于点( ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ,则
,则 ,其中
,其中 ;
;
⑤函数 的图像与直线
的图像与直线 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则 的取值范围为
的取值范围为 .
.
以上五个命题中正确的有 (填写所有正确命题的序号)
已知函数 ,则
,则 ( )
( )
A.最大值为2,且图象关于点 对称 对称 |
B.周期为 ,且图象关于点 ,且图象关于点 对称 对称 |
C.最大值为2,且图象关于 对称 对称 |
D.周期为 ,且图象关于点 ,且图象关于点 对称 对称 |
设函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)当 时,求
时,求 的取值范围.
的取值范围.