在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为 ,即
,即 给出四个结论:
给出四个结论:
①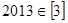 ,②
,② ,③
,③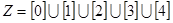 ,④整数
,④整数 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是 ,其中正确结论的个数是( )
,其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知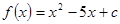 ,
, ,
, ,
,
若函数 不存在零点,则
不存在零点,则 的范围是 ( )
的范围是 ( )
A. |
B.  |
C. |
D. |
给定方程: ,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若
,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若 是该方程的实数解,则
是该方程的实数解,则
 –1.则正确命题是 .
–1.则正确命题是 .
对于函数 和
和
 ,下列说法正确的是 .
,下列说法正确的是 .
(1)函数 的图像关于直线
的图像关于直线 对称;
对称;
(2)
 的图像关于直线
的图像关于直线 对称;
对称;
(3)两函数的图像一共有10个交点;
(4)两函数图像的所有交点的横坐标之和等于30;
(5)两函数图像的所有交点的横坐标之和等于24.
已知函数 ,
, ,函数
,函数 的图像在点
的图像在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)求 的值;
的值;
(2)求函数 的极小值;
的极小值;
(3)设斜率为 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 ,(
,( )
)
证明: .
.
 表示不超过
表示不超过 的最大整数,定义函数
的最大整数,定义函数 .则下列结论中正确的有 .
.则下列结论中正确的有 .
①函数 的值域为
的值域为
②方程 有无数个解
有无数个解
③函数 的图像是一条直线
的图像是一条直线
④函数 是
是 上的增函数
上的增函数