高中数学函数迭代填空题

设 $\left[x\right]$表示不超 $x$的最大整数，（如 $\left[2\right]=2,\left[\frac{5}{4}\right]=1$）。对于给定的 $n\in N^{+}$,
定义 $C_n^x=\frac{n\left(n-1\right)\left(n-2\right)\dots \left(n-\left[x\right]+1\right)}{x\left(x-1\right)\dots \left(x-\left[x\right]+1\right)},x\in ,[1,+\infty )$则 $C_{\left[x\right]}^{\frac{3}{2}}=$ ;
当 $x\in [2,3)$时，函数 $C_8^x$的值域是 .

函数的一个零点是，则另一个零点是_________．

二次函数f(x)的二次项系数为正，且对任意实数x恒有f(2+x)=f(2－x),若f(1－2x²)<f(1+2x－x²),则x的取值范围是_________.

对于定义在上的函数，若存在距离为的两条直线和，使得对任意都有恒成立，则称函数有一个宽度为的通道.给出下列函数：
①；②；③；④
其中在区间上通道宽度可以为1的函数有          （写出所有正确的序号）.

已知二次函数f(x)=4x²－2(p－2)x－2p²－p+1,若在区间［－1，1］内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________.

给出以下四个结论：
①函数的对称中心是
②若不等式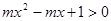对任意的x∈R都成立，则；
③已知点与点Q(l,0)在直线两侧，则；
④若将函数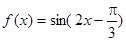的图像向右平移个单位后变为偶函数，则的最小值是．
其中正确的结论是____________（写出所有正确结论的编号）．

已知定义在上的偶函数满足对于恒成立，且，则 ________

在实数集中，我们定义的大小关系“”为全体实数排了一个“序”．类似实数排序的定义，我们定义“点序”记为“”：已知和，，当且仅当“”或“且”．定义两点的“”与“”运算如下：
．
则下面四个命题：
①已知和，则；
②已知和，若，则，且；
③已知，，则；
④已知，则对任意的点，都有；
⑤已知，则对任意的点，都有．
其中真命题的序号为              （把真命题的序号全部写出）

符号表示不超过的最大整数，如，定义函数，那么下列结论中正确的序号是         ．
①函数的定义域为，值域为；
②方程有无数解；
③函数是周期函数；
④函数在是增函数．

非零实数，满足，当取到最大值时，的值为
      ．

定义在上的函数，如果对于任意给定的等比数列， 仍是等比数列，则称为“保等比数列函数”．现有定义在上的如下函数：
①；  
②；   
③；   
④．
则其中是“保等比数列函数”的的序号为 __________．

已知函数的自变量取值区间为，若其值域也为，则称区间为的保值区间．若函数的保值区间是，则的值为            ．

定义在上的函数，其图象是连续不断的，如果存在非零常，使得对任意的，都有，则称为“倍增函数”，为“倍增系数”，下列命题为真命题的是  （写出所有真命题对应的序号）．
①若函数是倍增系数的倍增函数，则至少有1个零点；
②函数是倍增函数，且倍增系数；
③函数是倍增函数，且倍增系数．

设集合M＝｛f（x）｜存在实数t使得函数f(x)满足f(t+1)=f(t)＋f(1)｝，则下列函数(a,b,k都是常数）：
①；②；③；④.
其中属于集合M的函数是＿＿＿＿＿（填序号）．

方程 $x^2+x-1=0$的解可视为函数 $y=x^3+a$的图像与函数 $y=\frac{x}{4}$的图像交点的横坐标，若 $x^4+ax-4=0$的各个实根 $x_1$， $x_2$，…， $x_k$( $k$≤4)所对应的点( $x_i$)（ $i＝1,2,\dots ,k$）均在直线 $y=x$的同侧，则实数 $a$的取值范围是.