设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y),又当x2>x1>0时,f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范围.
对于在区间 上有意义的两个函数
上有意义的两个函数 ,如果对于任意的
,如果对于任意的 ,都有
,都有 则称
则称 在区间
在区间 上是“接近的”两个函数,否则称它们在区间
上是“接近的”两个函数,否则称它们在区间 上是“非接近的”两个函数。现有两个函数
上是“非接近的”两个函数。现有两个函数 给定一个区间
给定一个区间 。
。
(1)若 在区间
在区间 有意义,求实数
有意义,求实数 的取值范围;
的取值范围;
(2)讨论 在区间
在区间 上是否是“接近的”。
上是否是“接近的”。
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>-1,且当x∈[ ,
, )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.
已知曲线 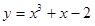 在点
在点 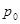 处的切线
处的切线 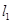 平行直线
平行直线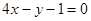 ,且点
,且点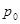 在第三象限.
在第三象限.
(Ⅰ)求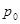 的坐标;
的坐标;
(Ⅱ)若直线 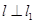 , 且
, 且  也过切点
也过切点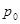 ,求直线
,求直线 的方程.
的方程.
已知函数 在
在 处取得极值,且
处取得极值,且 恰好是
恰好是 的一个零点.
的一个零点.
(Ⅰ)求实数 的值,并写出函数
的值,并写出函数 的单调区间;
的单调区间;
(Ⅱ)设 、
、 分别是曲线
分别是曲线 在点
在点 和
和 (其中
(其中 )处的切线,且
)处的切线,且 .
.
①若 与
与 的倾斜角互补,求
的倾斜角互补,求 与
与 的值;
的值;
②若 (其中
(其中 是自然对数的底数),求
是自然对数的底数),求 的取值范围.
的取值范围.
已知函数 在点
在点 处的切线方程为
处的切线方程为 .
.
(I)求 ,
, 的值;
的值;
(II)对函数 定义域内的任一个实数
定义域内的任一个实数 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.