.设集合 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合:
① ②
②
 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若 是等差数列,
是等差数列, 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
;
(Ⅱ)设数列 的通项为
的通项为 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列 的各项均为正整数,且
的各项均为正整数,且 ,试证
,试证 .
.
(本小题16分)如图所示,数列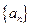 的前
的前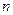 项的和
项的和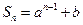 ,
,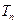 为数列
为数列 的前
的前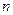 项的和,且
项的和,且 .
.
(1)求数列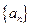 、
、 的通项公式;
的通项公式;
(2)找出所有满足: 的自然数
的自然数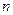 的值(不必证明);
的值(不必证明);
(3)若不等式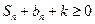 对于任意的
对于任意的 ,
,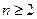 恒成立,求实数
恒成立,求实数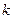 的最小值,并求出此时相应的
的最小值,并求出此时相应的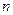 的值.
的值.
(本小题满分13分)已知数列 的前
的前 项和为
项和为 ,数列
,数列 满足
满足 ,
, .
.
(1)求数列 的通项公式; (2)求数列
的通项公式; (2)求数列 的前
的前 项和
项和 ;
;
(3)是否存在非零实数 ,使得数列
,使得数列 为等差数列,证明你的结论.
为等差数列,证明你的结论.
在数列{an}中,a1=1,an+1=can+cn+1(2n+1)(n∈N*),其中实数c≠0.求{an}的通项公式.
△ABC的三个内角A、B、C的对边的长分别为 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1) ;(2)
;(2) ;(3)
;(3) 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①_________________ _______
_______ __________________
__________________
②__________________________________________ (II)证明:
(II)证明:
已知数列{an}的前n项和为Sn,点(n,)在直线y=x+上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款( ),试用
),试用 和
和 表示小王第
表示小王第 (
( )个月的还款额
)个月的还款额 ;
;
(2)当 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月的工资的余额是否能满足此月 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: )
)
如下表定义函数f(x):
| x |
1 |
2 |
3 |
4 |
5 |
| f(x) |
5 |
4 |
3 |
1 |
2 |
对于数列{an},a1=4,an=f(an-1),n=2,3,4,…,求a2008.
已知正数数列 中,
中, ,前
,前 项和为
项和为 ,对任意
,对任意 ,
, 、
、 、
、 成等差数列.
成等差数列.
(1)求 和
和 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,当
,当 时,证明:
时,证明: .
.