设函数f(x)=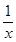 ,g(x)=-x2+bx.若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
,g(x)=-x2+bx.若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
| A.x1+x2>0,y1+y2>0 |
| B.x1+x2>0,y1+y2<0 |
| C.x1+x2<0,y1+y2>0 |
| D.x1+x2<0,y1+y2<0 |
根据表格中的数据,可以断定方程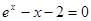 的一个根所在的区间是( )
的一个根所在的区间是( )
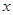 |
-1 |
0 |
1 |
2 |
3 |
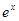 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
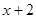 |
1 |
2 |
3 |
4 |
5 |
A.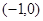 B.
B.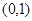 C.
C.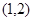 D.
D.
若函数
 有极值点
有极值点 ,且
,且 ,则关于
,则关于 的方程
的方程 的不同实根的个数是( )
的不同实根的个数是( )
| A.5 | B.4 | C.3 | D.2 |
已知函数 ,给出下列结论:
,给出下列结论:
① 是
是 的单调递减区间;
的单调递减区间;
②当 时,直线
时,直线 与
与 的图象有两个不同交点;
的图象有两个不同交点;
③函数 的图象与
的图象与 的图象没有公共点.
的图象没有公共点.
其中正确的序号是( )
| A.①②③ | B.①③ | C.①② | D.②③ |
(本题满分14分,第1小题6分,第2小题8分)
已知函数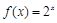 的反函数为
的反函数为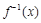
(1)若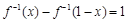 ,求实数
,求实数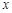 的值;
的值;
(2)若关于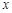 的方程
的方程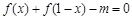 在区间
在区间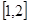 内有解,求实数
内有解,求实数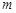 的取值范围;
的取值范围;
定义 ,若关于
,若关于 的方程
的方程
 有三个不同的实根
有三个不同的实根 ,则
,则
A.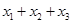 有最小值, 有最小值, 无最大值 无最大值 |
B.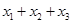 无最小值, 无最小值, 有最大值 有最大值 |
C.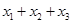 有最小值, 有最小值, 有最大值 有最大值 |
D.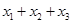 无最小值, 无最小值, 无最大值 无最大值 |