已知定义在R上的函数 的对称轴为
的对称轴为 ,且当
,且当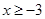 时,
时, ,若函数
,若函数 在区间
在区间
 上有零点,则k的值为( )
上有零点,则k的值为( )
| A.2或-7 | B.2或-8 | C.1或-7 | D.1或-8 |
已知定义在R上的偶函数f(x)满足f(4-x)=f(x),且当x∈(-1,3]时,f(x)= ,则函数g(x)=f(x)-|lgx|的零点个数是( )
,则函数g(x)=f(x)-|lgx|的零点个数是( )
| A.7 | B.8 | C.9 | D.10 |
已知 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程 (
( 且
且 )有
)有 个不同的根,则
个不同的根,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2 000元.
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
已知函数 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得函数恰有2个不同的零点;
,使得函数恰有2个不同的零点;
②存在实数 ,使得函数恰有4个不同的零点;
,使得函数恰有4个不同的零点;
③存在实数 ,使得函数恰有5个不同的零点;
,使得函数恰有5个不同的零点;
④存在实数 ,使得函数恰有8个不同的零点.
,使得函数恰有8个不同的零点.
其中真命题的序号是 (把你认为正确的序号全写上).
(把你认为正确的序号全写上).
设 ,已知函数
,已知函数 的定义域是
的定义域是 ,值域是
,值域是 ,若函数
,若函数 有唯一的零点,则
有唯一的零点,则 ( )
( )
| A.2 | B. |
C.1 | D.0 |