高中数学不定方程和方程组填空题

关于方程有唯一的解，则实数的取值范围是________.

已知函数有三个零点，则实数的取值范围为.

对于实数和，定义运算“”：，设，且关于的方程为恰有三个互不相等的实数根，则的取值范围是___________.

给出下列四个命题：
①命题“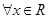，”的否定是“，”；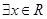
②已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是；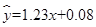
③圆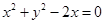的圆心到直线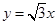的距离是；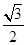
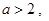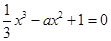④若则方程在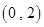上恰好有1个根；
⑤对于大于1的自然数m的二次幂可以用技术进行以下方式的“分裂”：……仿此，若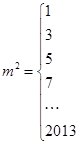，则m=1007；
其中真命题的序号是                 .（填上所有真命题的序号）

给出下列四个命题：
①命题“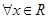，”的否定是“，”；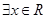
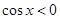②若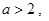则方程在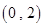上恰好有1个根；
③如果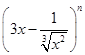的展开式中二项式系数之和为128，则展开式中的系数是；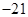
④由直线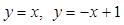，及x轴围成平面图形的面积为；
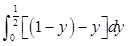其中真命题的序号是                 .（填上所有真命题的序号）

已知关于x的方程x²＋2alog₂(x²＋2)＋a²－3＝0有唯一解，则实数a的值为________．

我们把形如y＝ (a>0，b>0)的函数因其图象类似于汉字中的“囧”字，故生动地称为“囧函数”，若当a＝1，b＝1时的“囧函数”与函数y＝lg|x|的交点个数为n，则n＝________.

已知函数f(x)＝，若函数g(x)＝f(x)－k有两个不同的零点，则实数k的取值范围是________．

已知函数，关于的方程（）恰有6个不同实数解，则的取值范围是     ．

对于函数的定义域为D,如果存在区间同时满足下列条件:
①在[m,n]是单调的;②当定义域为[m,n]时, 的值域也是[m,n],则称区间[m,n]是该函数的“H区间”.若函数存在“H区间”,则正数的取值范围是____________.

若关于的方程有四个不同的实数解，则实数k的取值范围是        .

已知函数f(x)=4解集为空集，则满足条件的实数a的值为          .

设函数与的图象的交点为，且，则=      .

若时，函数在上有且只有一个零点，则=   

若函数在给定区间M上存在正数t，使得对于任意，有，且，则称为M上的t级类增函数。给出4个命题
①函数上的3级类增函数
②函数上的1级类增函数
③若函数上的级类增函数，则实数a的最小值为2
④设是定义在上的函数，且满足：1.对任意，恒有；2.对任意，恒有；3. 对任意，，若函数是上的t级类增函数，则实数t的取值范围为。
以上命题中为真命题的是