已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
已知p:方程2x2-2mx+1=0有两个不相等的负实根;q:存在x∈R,
x2+mx+1<0.若p或q为真,p且q为假,求实数m的取值范围.
(本小题满分16分)已知 为
为 上的奇函数,当
上的奇函数,当 时,
时, 为二次函数,且满足
为二次函数,且满足 ,不等式组
,不等式组 的解集是
的解集是 .
.
(1)求函数 的解析式;
的解析式;
(2)作出 的图象并根据图象讨论关于
的图象并根据图象讨论关于 的方程:
的方程:
 根的个数.
根的个数.
设函数fn(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间 内存在唯一零点;
内存在唯一零点;
(2)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围;
(3)在(1)的条件下,设xn是fn(x)在 内的零点,判断数列x2,x3,…,xn,…的增减性.
内的零点,判断数列x2,x3,…,xn,…的增减性.
(本小题满分13分)函数 (
( 为常数)的图象过点
为常数)的图象过点 .
.
(1)求 的值;
的值;
(2)函数 在区间
在区间 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 (
( 为常数)的正根的个数.
为常数)的正根的个数.
设 .
.
(1)若函数 在
在 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
(2)设 .
.
①证明:函数 有3个零点;
有3个零点;
②若存在实数 ,当
,当 时函数
时函数 的值域为
的值域为 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,函数
,函数 .
.
(1)当 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
(2)当 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数 的图象的公共点的个数;
的图象的公共点的个数;
(3)函数 的图象能否恒在函数
的图象能否恒在函数 的图象的上方?若能,求出
的图象的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
(本小题满分14分)已知 为常数,且
为常数,且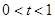 ,函数
,函数 的最小值和函数
的最小值和函数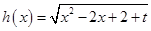 的最小值都是函数
的最小值都是函数
 R
R 的零点.
的零点.
(1)用含 的式子表示
的式子表示 ,并求出
,并求出 的取值范围;
的取值范围;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.