为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200 只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
表2:注射药物B后皮肤疱疹面积的频数分布表
完成下面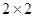 列联表,并回答能否有99.9﹪的把握认为“注射药物A后的皮肤疱疹面积与注射药物B后的皮肤疱疹面积有差异”。
列联表,并回答能否有99.9﹪的把握认为“注射药物A后的皮肤疱疹面积与注射药物B后的皮肤疱疹面积有差异”。
表3:
|
疱疹面积小于70mm2
|
疱疹面积不小于70mm2
|
合计
|
注射药物A
|
a=
|
b=
|
|
注射药物B
|
c=
|
d=
|
|
合计
|
|
|
n=
|
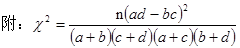
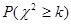
|
0.100
|
0.050
|
0.025[
|
0.010
|
0.001
|
k
|
2.706
|
3.841
|
5.024
|
6.635
|
10.828
|