已知
(I)a=2时,求 和
和 的公共点个数;
的公共点个数;
(II)a为何值时, 的公共点个数恰为两个。
的公共点个数恰为两个。
线段y= l,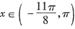 与函数
与函数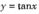 ,
,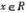 ,
, 图象的交点个数是
图象的交点个数是
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,若a
,若a 、b、c均不相等且
、b、c均不相等且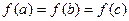 ,则abc的取值范围为 ( )
,则abc的取值范围为 ( )
| A.(1,10) | B.(5,6) | C.(10,15) | D.(20,24) |
:已知函数 ,关于
,关于 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中真命题的序号为______▲_______.
若关于x的方程 在R上都有解,则
在R上都有解,则 的最小值为:( )
的最小值为:( )
| A.256 | B. 128 | C. 64 | D.32 |
已知 实数
实数 、
、 、
、 满足
满足 ,(0<
,(0< <
< <
< )若实数
)若实数 是函数
是函数 的一个零点,那么下列不等式中,不可能成立的是 ( )
的一个零点,那么下列不等式中,不可能成立的是 ( )
A. |
B. |
C. |
D. |
已知函数 是R 上的偶函数,且在(0,+
是R 上的偶函数,且在(0,+ )上有
)上有 (x)> 0,若f(-1)= 0,那么关于x的不等式x f(x)< 0 的解集是____________.
(x)> 0,若f(-1)= 0,那么关于x的不等式x f(x)< 0 的解集是____________.