高中数学不定方程和方程组试题

对于实数和，定义运算“”：，设，且关于的方程为恰有三个互不相等的实数根，则的取值范围是___________．

已知函数f（x）满足f（x）＝f（），当x∈[1，3]时，f（x）＝lnx，若在区间[，3]内，曲线g（x）＝f（x）－ax与x轴有三个不同的交点，则实数a的取值范围是（ ）.

A．（0，）

B．（0，）

C．[，）

D．[，）

已知等比数列的首项，其前四项恰是方程 的四个根，则            .

已知等比数列的首项，其前四项恰是方程 的四个根，则            .

直线与曲线相切，则的值为（     ）  

A．－2

B．－1

C．－

D．1

已知函数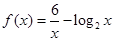，在下列区间中，包含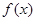的零点的区间是（   ）

A．（0，1）	B．（1，2）
C．（2，4）	D．（4，＋∞）

已知函数，则在下列区间中，函数有零点的是（    ）

A．

B．

C．

D．

【原创】下列命题中，真命题的序号是              ．
①函数的零点只有1个且属于区间
②数列的前n项和，则数列是等差数列．
③函数的图像与函数的图像有3个不同的交点．
④等差数列前n项和为,已知,则m=10．

设函数＝||＋b＋c，给出下列四个命题：
①若是奇函数，则c＝0
②b＝0时，方程＝0有且只有一个实根
③的图象关于（0，c）对称
④若b0，方程＝0必有三个实根
其中正确的命题是         （填序号）

已知为上的偶函数，对任意都有且当，时，有成立，给出四个命题：①；②直线是函数的图像的一条对称轴；③函数在上为增函数；④函数在上有四个零点，其中所有正确命题的序号为          ．

已知，求证：关于的三个方程，，中至少有一个方程有实数根.

已知函数（，为常数），当时，函数有极值，若函数有且只有三个零点，则实数的取值范围是        ．

函数f(x)=e^x+x－2的零点所在的一个区间是（  ）

A．(－2, －1)

B．(－1, 0)

C．(0, 1)

D．(1, 2)

方程有实根，则实数b的取值范围是            .

已知函数f（x）=lgx+x-10的零点在区间（k,k+1）上，则k=            .