(本小题满分10分)
命题p:对任意实数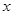 都有
都有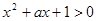 恒成立;命题q :关于
恒成立;命题q :关于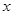 的方程
的方程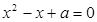 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数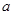 的取值范围。
的取值范围。
判断下列语句是不是命题,如果k,,,是,说明是全称命题还是特称命题.
(1) 任何一个实数除以1,仍等于这个数;
(2) 三角函数都是周期函数吗?
(3) 有一个实数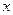 ,
,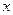 不能取倒数;
不能取倒数;
(4) 有的三角形内角和不等于
设命题p:函数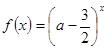 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在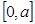 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求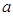 的取值范围.
的取值范围.
本小题12分)命题p: 函数y=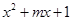 在(-1, +
在(-1, + )上单调递增, 命题
)上单调递增, 命题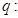 函数y=lg[
函数y=lg[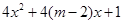 ]的定义域为R
]的定义域为R
(1) 若“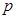 或
或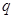 ”为真命题,求
”为真命题,求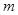 的取值范围;
的取值范围;
(2) 若“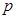 或
或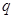 ”为真命题,“
”为真命题,“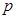 且
且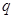 ”为假命题,求
”为假命题,求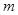 的取值范围
的取值范围
已知命题p:“ x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“ x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
在一次模拟射击游戏中,小李连续射击了两次,设命题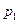 :“第一次射击中靶”,命题
:“第一次射击中靶”,命题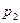 :“第二次射击中靶”,试用
:“第二次射击中靶”,试用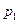 ,
,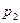 及逻辑连结词“或”“且”“非”表示下列命题:
及逻辑连结词“或”“且”“非”表示下列命题:
(1)两次射击均中靶; (2)两次射击均未中靶; 

(3)两次射击恰好有一次中靶;(4)两次射击至少有一次中靶.
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[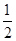 ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+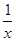 >
>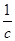 恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
已知a>0且a≠1,设命题p:函数y=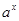 +1在R上单调递减,命题q:曲线y=
+1在R上单调递减,命题q:曲线y=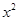 +(2a-3)x+1与x轴交于不同的两点,如果“p∨q”为真,且“p∧q”为假,求a的取值范围.
+(2a-3)x+1与x轴交于不同的两点,如果“p∨q”为真,且“p∧q”为假,求a的取值范围.