2013年高考数学预测题 第五期(2013年5月上)
设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是( )
| A.(-∞,0] | B.[2,+∞) |
| C.(-∞,0]∪[2,+∞) | D.[0,2] |
在△ABC中,sin2A≤sin2B+sin2C-sinBsinC,则A的取值范围是( )
A.(0, ] ] |
B.[ ,π) ,π) |
C.(0, ] ] |
D.[ ,π) ,π) |
已知点O(0,0),B(3,0),C(4, ),向量
),向量 =
= ,E为线段DC上的一点,且四边形OBED为等腰梯形,则向量
,E为线段DC上的一点,且四边形OBED为等腰梯形,则向量 等于( )
等于( )
A.(2, ) ) |
B.(2, )或 )或 |
C. |
D.(2, )或(3, )或(3, ) ) |
如图,平面α⊥平面β,α∩β=直线 ,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线
,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线 ,M,N分别是线段AB,CD的中点.下列判断正确的是( )
,M,N分别是线段AB,CD的中点.下列判断正确的是( )
| A.当|CD|=2|AB|时,M,N两点不可能重合 |
B.M,N两点可能重合,但此时直线AC与 不可能相交 不可能相交 |
C.当AB与CD相交,直线AC平行于 时,直线BD可以与 时,直线BD可以与 相交 相交 |
D.当AB,CD是异面直线时,直线MN可能与 平行 平行 |
一条光线沿直线 入射到直线
入射到直线 后反射,则反射光线所在的直线方程为( )
后反射,则反射光线所在的直线方程为( )
| A.2x+y-6=0 | B.x-2y+7=0 |
| C.x-y+3=0 | D.x+2y-9=0 |
过椭圆 +
+ =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
A. |
B. |
C. |
D. |
某地一农业科技试验站,对一批新水稻种子进行试验.已知这批水稻种子的发芽率为0.8,出芽后的幼苗成活率为0.9,在这批水稻种子中,随机地抽取一粒,则这粒水稻种子能成长为幼苗的概率为( )
| A.0.02 | B.0.08 |
| C.0.18 | D.0.72 |
若命题“∃x∈R,2x2-3ax+9<0”为假命题,则实数a的取值范围是____________.
已知函数f(x)=log3(a-3x)+x-2,若f(x)存在零点,则实数a的取值范围是________.
已知数列{an}的前n项和为Sn,且Sn=n2+n,数列{bn}满足bn= (n∈N*),Tn是数列{bn}的前n项和,则T9等于________.
(n∈N*),Tn是数列{bn}的前n项和,则T9等于________.
如下图为一个几何体的三视图,其中俯视图为正三角形,其中A1B1=2,AA1=4,则该几何体的表面积为 .
如图,直角坐标系xOy所在的平面为α,直角坐标系x′Oy′(其中y′与y轴重合)所在平面为β,∠xOx′=45°.
(1)已知平面β内有一点P′(2 ,2),则点P′在平面α内的射影P的坐标为________;
,2),则点P′在平面α内的射影P的坐标为________;
(2)已知平面β内的曲线C′的方程是(x′- )2+2y′2-2=0,则曲线C′在平面α内的射影C的方程是________.
)2+2y′2-2=0,则曲线C′在平面α内的射影C的方程是________.
设命题p:函数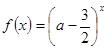 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在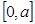 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求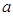 的取值范围.
的取值范围.
已知数列{an}的前n项和为Sn,且对任意的n∈N*有an+Sn=n.
(1)设bn=an-1,求证:数列{bn}是等比数列;
(2)设c1=a1且cn=an-an-1(n≥2),求{cn}的通项公式.
已知定义在区间[- ,
, ]上的函数y=f(x)图像关于直线x=
]上的函数y=f(x)图像关于直线x= 对称,当x≥
对称,当x≥ 时,f(x)=-sinx.
时,f(x)=-sinx.
(1)作出y=f(x)的图像;
(2)求y=f(x)的解析式.
已知正项数列{an}中,a1=6,且an+1=an+1;数列{bn}中,点Bn(n,bn)在过点(0,1)且以(1,2)为方向向量的直线l上.
(1)求数列{an},{bn}的通项公式;
(2)若f(n)= 问是否存在k∈N*,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,请说明理由.
问是否存在k∈N*,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,请说明理由.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1= ,BB1=2.
,BB1=2.
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1.
已知圆C过点P(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)设Q为圆C上的一个动点,求 ·
· 的最小值;
的最小值;
(3)过点P作两条相异直线分别与圆C相交于A、B,且直线PA与直线PB的倾斜角互补.O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
已知过抛物线y2=2px(p>0)的焦点,斜率为2 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 =
= +λ
+λ ,求λ的值.
,求λ的值.
一次数学模拟考试,共12道选择题,每题5分,共计60分.小张所在班级共有40人,此次考试选择题得分情况统计表:
| 得分(分) |
40 |
45 |
50 |
55 |
60 |
| 百分率 |
15% |
10% |
25% |
40% |
10% |
现采用分层抽样的方法从此班抽取20人的试卷进行选择题质量分析.
(1)应抽取多少张选择题得60分的试卷?
(2)若小张选择题得60分,求他的试卷被抽到的概率.
设不等式|2x-1|<1的解集为M.
(1)求集合M;
(2)若a,b∈M,试比较ab+1与a+b的大小.
 ,则a3=( )
,则a3=( )

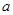 、
、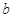 、
、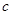 是正实数,且
是正实数,且 ,则
,则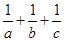 的最小值为( )
的最小值为( )


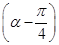 =
=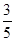 ,α∈
,α∈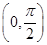 ,则sinα=________.
,则sinα=________. }满足:
}满足: =
= +2
+2 ,若存在两项
,若存在两项 ,
, ,则
,则 +
+ 的最小值为________.
的最小值为________. ),渐近线方程为y=±
),渐近线方程为y=± x的双曲线的方程为________.
x的双曲线的方程为________. )20的二项展开式中,
)20的二项展开式中, 的系数与
的系数与 的系数之差为________.
的系数之差为________. (a∈R且a≠0),试求函数f(x)的极大值与极小值.
(a∈R且a≠0),试求函数f(x)的极大值与极小值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号