已知过抛物线y2=2px(p>0)的焦点,斜率为2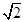 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若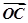 =
=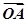 +λ
+λ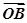 ,求λ的值.
,求λ的值.
推荐套卷
已知过抛物线y2=2px(p>0)的焦点,斜率为2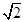 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若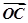 =
=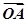 +λ
+λ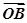 ,求λ的值.
,求λ的值.