已知正项数列{an}中，a1＝6，且an＋1＝an＋1；数列{bn}中，点Bn(n，bn)在过点(0,1)且以(1,2)为方向向量的直线l上．
(1)求数列{an}，{bn}的通项公式；
(2)若f(n)＝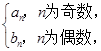
问是否存在k∈N*，使f(k＋27)＝4f(k)成立，若存在，求出k值；若不存在，请说明理由．
相关试题
是二次函数，方程
有两个相等实根，且
，求
的表达式．
，求：（1）在
之间的平均速度（设
）；
时的瞬时速度．
km处的海岸渔站中，如果送信人步行每小时5km，船速每小时4km，问应在何处登岸可以使抵达渔站的时间最省？
．推荐套卷
已知正项数列{an}中，a1＝6，且an＋1＝an＋1；数列{bn}中，点Bn(n，bn)在过点(0,1)且以(1,2)为方向向量的直线l上．
(1)求数列{an}，{bn}的通项公式；
(2)若f(n)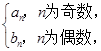＝问是否存在k∈N*，使f(k＋27)＝4f(k)成立，若存在，求出k值；若不存在，请说明理由．
粤公网安备 44130202000953号