(本题满分14分,第1小题满分4分,第2小题满分4分,第3小题满分6分)
设函数 ,
,
(1)求 的反函数
的反函数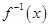 ;
;
(2)判断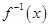 的单调性,不必证明;
的单调性,不必证明;
(3)令 ,当
,当

 ,
, 时,
时,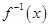 在
在 上的值域是
上的值域是 ,求
,求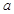 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求满足
时,求满足 的
的 的取值范围;
的取值范围;
(2)若 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 的解析式,判断其在R上的单调性并加以证明.
的解析式,判断其在R上的单调性并加以证明.
已知函数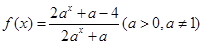 是定义在R上的奇函数.
是定义在R上的奇函数.
(I)求实数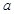 的值;
的值;
(II)判断 在定义域上的单调性,并用单调性定义证明;
在定义域上的单调性,并用单调性定义证明;
(III)当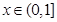 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知:函数f(x)=ax(0<a<1),
(Ⅰ)若f(x )=2,求f(3x
)=2,求f(3x );
);
(Ⅱ)若f(2x -3x+1)
-3x+1) f(x
f(x +2x-5),求x的取值范围。
+2x-5),求x的取值范围。