高中数学随机思想的发展解答题

（本小题满分12分）
东莞市政府要用三辆汽车从新市政府把工作人员接到老市政府，已知从新市政府到老市政府有两条公路，汽车走公路①堵车的概率为，不堵车的概率为；汽车走公路②堵车的概率为，不堵车的概率为．若甲、乙两辆汽车走公路①，丙汽车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．
（1）若三辆汽车中恰有一辆汽车被堵的概率为，求走公路②堵车的概率；
（2）在（1）的条件下，求三辆汽车中被堵车辆的个数的分布列和数学期望．

（本小题满分14分）甲、乙两间商店购进同一种商品的价格均为每件30元，销售价均为每件50元．根据前5年的有关资料统计，甲商店这种商品的年需求量服从以下分布：

	10	20	30	40	50
	0.15	0.20	0.25	0.30	0.10

乙商店这种商品的年需求量服从二项分布．
若这种商品在一年内没有售完，则甲商店在一年后以每件25元的价格处理；乙商店一年后剩下的这种商品第1件按25元的价格处理，第2件按24元的价格处理，第3件按23元的价格处理，依此类推．今年甲、乙两间商店同时购进这种商品40件，根据前5年的销售情况，请你预测哪间商店的期望利润较大？

某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进入第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品合格的概率依次为，，，经过第二次烧制后，甲、乙、丙三件产品合格的概率依次为，，．（1）求第一次烧制后恰有一件产品合格的概率；
（2）经过前后两次烧制后，合格工艺品的个数为，求随机变量的期望         

设排球队A与B进行比赛，规定若有一队胜四场，则为获胜队，已知两队水平相当
（1）求A队第一、五场输，第二、三、四场赢，最终获胜的概率；
（2）若要决出胜负，平均需要比赛几场？

某批数量较大的商品的次品率是5％，从中任意地连续取出10件，为所含次品的个数，求．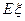
分析：数量较大，意味着每次抽取时出现次品的概率都是0.05，可能取值是：0，1，2，…，10．10次抽取看成10次独立重复试验，所以抽到次品数服从二项分布，由公式可得解．

有n把看上去样子相同的钥匙，其中只有一把能把大门上的锁打开．用它们去试开门上的锁．设抽取钥匙是相互独立且等可能的．每把钥匙试开后不能放回．求试开次数的数学期望和方差．
分析：求时，由题知前次没打开，恰第k次打开．不过，一般我们应从简单的地方入手，如，发现规律后，推广到一般

(本题满分12分)有人预测:在2010年的广州亚运会上,排球赛决赛将在中国队与日本队之间展开,据以往统计, 中国队在每局比赛中胜日本队的概率为,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.（Ⅰ）求中国队以3:1获胜的概率;（Ⅱ）设表示比赛的局数,求的期望值.

(本小题满分12分)   不透明盒中装有10个形状大小一样的小球，其中有2个小球上标有数字1，有3个小球上标有数字2，还有5个小球上标有数字3．取出一球记下所标数字后放回，再取一球记下所标数字，共取两次．设两次取出的小球上的数字之和为ξ．
(Ⅰ)求随机变量ξ的分布列；    (Ⅱ)求随机变量ξ的期望Eξ．

（本小题满分12分）设是一个离散型随机变量，其分布列如下表，试求随机变量的期望与方差．

ξ	－1	0	1
P		1－2q	q^2

 

(本小题满分12分)学网某种家用电器每台的销售利润与该电器的无故障使用时间 (单位：年)有关. 若，则销售利润为元；若，则销售利润为元；若，则销售利润为元．设每台该种电器的无故障使用时间，及这三种情况发生的概率分别为，，，叉知，是方程的两个根，且（1）求，，的值；（2）记表示销售两台这种家用电器的销售利润总和，求的期望.

（(12分)大学毕业生小明到甲、乙、丙三个单位应聘，其被录用的概率分别为（各单位是否录用他相互独立，允许小明被多个单位同时录用） （1）求小明没有被录用的概率；（2）设录用小明的单位个数为，求的分布列和它的数学期望。

在1，2，3…，9，这9个自然数中，任取3个数.
（Ⅰ）求这3个数中，恰有一个是偶数的概率；  
（Ⅱ）记 $\xi$为这三个数中两数相邻的组数，（例如：若取出的数1、2、3，则有两组相邻的数1、2和2、3，此时 $\xi$的值是2）。求随机变量 $\xi$的分布列及其数学期望 $E\xi$

将数字分别写在大小、形状都相同的张卡片上，将它们反扣后（数字向下），再从左到右随机的依次摆放，然后从左到右依次翻卡片：若第一次就翻出数字则停止翻卡片；否则就继续翻，若将翻出的卡片上的数字依次相加所得的和是的倍数则停止翻卡片；否则将卡片依次翻完也停止翻卡片．设翻卡片停止时所翻的次数为随机变量，求出的分布列和它的数学期望．

某公司“咨询热线”电话共有10路外线，经长期统计发现，在8点至10点这段时间内，英才苑外线电话同时打入情况如下表所示：

电话同时打入数ξ	0	1	2	3	4	5	6	7	8	9	10
概率P	0.13	0.35	0.27	0.14	0.08	0.02	0.01	0	0	0	0

  （1）若这段时间内，公司只安排了2位接线员（一个接线员一次只能接一个电话）.
①求至少一路电话不能一次接通的概率；
②在一周五个工作日中，如果有三个工作日的这一时间内至少一路电话不能一次接通，那么公司的形象将受到损害，现用至少一路电话一次不能接通的概率表示公司形象的“损害度”，求这种情况下公司形象的“损害度”；（2）求一周五个工作日的这一时间内，同时打入的电话数ξ的期望值.

（本小题满分12分）某休闲会馆拟举行“五一”应祝活动，每位来宾交30元的入场费，可参加一次抽奖活动. 抽奖活动规则是：从一个装有分值分别为1，2，3，4，5，6的六个相同小球的抽奖箱中，有放回的抽取两次，每次抽取一个球，规定：若抽得两球的分值和为12分，则获得价值为m元的礼品；若抽得两球的分值和为11分或10分，则获得价值为100元的礼品；若抽得两球的分值和低于10分，则不获奖.  （1）求每位会员获奖的概率；（2）假设会馆这次活动打算即不赔钱也不赚钱，则m应为多少元？