(本小题满分12分)某休闲会馆拟举行“五一”应祝活动,每位来宾交30元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为1,2,3,4,5,6的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值和为12分,则获得价值为m元的礼品;若抽得两球的分值和为11分或10分,则获得价值为100元的礼品;若抽得两球的分值和低于10分,则不获奖. (1)求每位会员获奖的概率;(2)假设会馆这次活动打算即不赔钱也不赚钱,则m应为多少元?
相关知识点
推荐套卷
 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.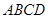 中,对角线
中,对角线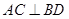 于
于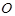 ,
,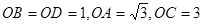 ,
,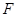 为
为 的重心,过点
的重心,过点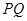 分别交
分别交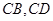 于
于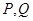 且
且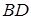 ,沿
,沿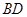 将
将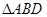 折起,沿
折起,沿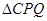 折起,
折起,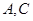 正好重合于
正好重合于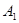 .
. 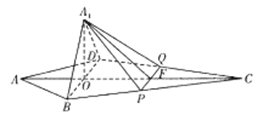
 平面
平面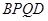 ;
; 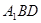 与平面
与平面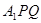 夹角的大小.
夹角的大小.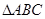 中,角
中,角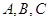 的对边分别为
的对边分别为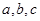 ,且向量
,且向量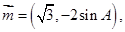
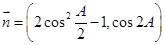 ,且
,且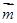 ‖
‖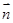 ,
,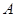 为锐角.
为锐角.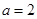 ,
, ,求
,求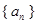 是首项为
是首项为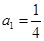 ,公比
,公比 的等比数列. 设
的等比数列. 设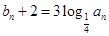
 ,数列
,数列 满足
满足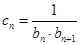 .
. 成等差数列;
成等差数列; 项和
项和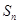 .
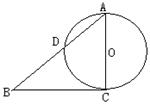
.
 与直线
与直线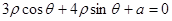 相切,求实数a的值______.
相切,求实数a的值______.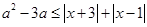 对任意实数
对任意实数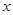 恒成立,求实数
恒成立,求实数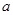 的取值范围____.
的取值范围____. 粤公网安备 44130202000953号
粤公网安备 44130202000953号