高中数学随机思想的发展解答题

为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．

（1）求该校报考飞行员的总人数；
（2）以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选三人，设表示体重超过60公斤的学生人数，求的分布列和数学期望．

心理学家分析发现视觉和空间能力与性别有关， 某数学兴趣小组为了 验 证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学 （男30女20）， 给所有同学几何题和代数题各一题， 让各位同学自由选择一道题进行解答．选题情况如下表：（单位：人）

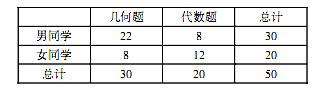
（Ⅰ）能否据此判断有97．5%的把握认为视觉和空间能力与性别有关？
（Ⅱ）经过多次测试后，甲每次解答一道几何题所用的时间在5—7分钟，乙每次解答一道几何题所用
的时间在6—8分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．
（Ⅲ）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、 乙两女
生被抽到的人数为X， 求X的分布列及数学期望E（X） ．
附表及公式

在一个盒子中，放有大小相同的红、白、黄三个小球，从中任意摸出一球，若是红球记分，白球记分，黄球记分．现从这个盒子中，有放回地先后摸出两球，所得分数分别记为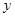，，设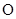为坐标原点，点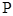的坐标为，记．
（1）求随机变量的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望．

（本小题满分12分）某商家对他所经销的一种商品的日销售量（单位：吨）进行统计，最近50天的统计结果如下表：

日销售量	1	1．5	2
天数	10	25	15
频率

 
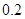若以上表中频率作为概率，且每天的销售量相互独立．
（1）求5天中该种商品恰好有两天的销售量为1．5吨的概率；
（2）已知每顿该商品的销售利润为2千元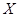，表示该种商品某两天销售利润的和（单位：千元），求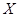的分布列和数学期望．

（本小题满分12分）为了提高我市的教育教学水平，市教育局打算从红塔区某学校推荐的10名教师中任选3人去参加支教活动。这10名教师中，语文教师3人，数学教师4人，英语教师3人．
求：（1）选出的语文教师人数多于数学教师人数的概率；
（2）选出的3人中，语文教师人数的分布列和数学期望．

有一种密码，明文由三个字母组成，密码由明文的这三个字母对应的五个数字组成．编码规则如下表．明文由表中每一排取一个字母组成，且第一排取的字母放在第一位，第二排取的字母放在第二位，第三排取的字母放在第三位，对应的密码由明文所取的三个字母对应的数字按相同的次序排成一组组成．（如：明文取的三个字母为AFP，则与它对应的五个数字（密码）就为11223）

第一排	明文字母	A	B	C
密码数字	11	12	13
第二排	明文字母	E	F	G
密码数字	21	22	23
第三排	明文字母	M	N	P
密码数字	1	2	3

 
（1）假设密码是11211，求这个密码对应的明文；
（2）设随机变量表示密码中所含不同数字的个数．
①求；②求随机变量的分布列和数学期望．

（本小题满分12分）某地宫有三个通道，进入地宫的每个人都要经过一扇智能门。首次到达此门，系统会随机（即等可能）为你打开一个通道，若是1号通道，则需要1小时走出地宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门。再次到达智能门时，系统会随机打开一个你未到过的通道，直至走完地宫为止。令表示走出地宫所需的时间。
（1）求的分布列； 
（2）求的数学期望。

（本小题满分12分）某班同学利用国庆节进行社会实践，对 [25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：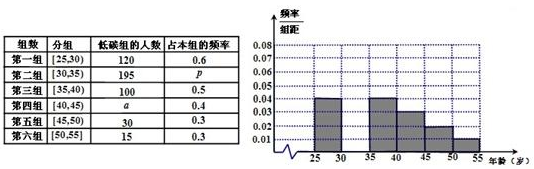

（1）补全频率分布直方图并求n、a、p的值；
（2）从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和期望E（X）．

2015年春节期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中，按进服务区的先后每间隔辆就抽取一辆的抽样方法，抽取了名驾驶员进行调查，将他们在某段高速公路上的车速（km/t）分成6段：，，，，，后得到如图４的频率分布直方图．问：

（1）该公司在调查取样中，用到的是什么抽样方法？
（2）求这40辆小型汽车车速的众数和中位数的估计值；
（3）若从车速在中的车辆中任取2辆，求抽出的这两辆车中速度在中的车辆数的分布列及其数学期望．

（本小题满分12分）甲、乙两袋中各装有大小相同的小球个，其中甲袋中红色、黑色、白色小球的个数分别为、、，乙袋中红色、黑色、白色小球的个数均为，某人用左右手分别从甲、乙两袋中取球．
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若左右手依次各取两球，称同一手中两球颜色相同的取法为成功取法，记两次取球的成功取法次数为随机变量，求的分布列和数学期望．

（本小题满分12分）为调查高三学生的视力情况，某高中学生会从全体学生中随机抽取16名学生，经校医用视力表检测得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶），如图，若视力测试结果不低于5．0，则称为“好视力”。
  
（1）写出这组数据的众数和中位数；
（2）从这16人中随机选取3人，求至少有2人是“好视力”的概率；
（3）以这16人的样本数据来估计整个学校的总体数据，若从该校（人数很多）任选3人，记X表示抽到“好视力”学生的人数，求X的分布列及数学期望。

（本小题满分12分）某工厂生产甲、乙两种芯片，其质量按测试指标划分为：指标大于或等于82为合格品，小于82为次品．现随机抽取这两种芯片各100件进行检测，检测结果统计如下：

（Ⅰ）试分别估计芯片甲，芯片乙为合格品的概率；
（Ⅱ）生产一件芯片甲，若是合格品可盈利40元，若是次品则亏损5元；生产一件芯片乙，若是合格品可盈利50元，若是次品则亏损10元．在（Ⅰ）的前提下，记X为生产1件芯片甲和1件芯片乙所得的总利润，求随机变量X的概率分布列和数学期望值．

（本小题满分12分）已知2件次品和3件正品混放在一起，现需要通过检测将其区分，
每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测
结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）己知每检测一件产品需要费用1 00元，设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用（单位：元），求X的分布列和均值（数学期望）．

（本小题满分12分）某批发市场对某种商品的日销售量（单位：吨）进行统计，最近50天的
统计结果如下：

日销售量（吨）	1	1．5	2
频数	10	25	15
频率	0．2

（1）求表中的的值；
（2）若以上表频率作为概率，且每天的销售量相互独立．求:
①5天中该种商品恰好有2天的销售量为1．5吨的概率;
②已知每吨该商品的销售利润为2千元,表示该种商品两天销售利润的和（单位:千元）求的分布列和期望．

（本小题满分12分）某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为，得到乙公司和丙公司面试的概率均为p，，且三个公司是否让其面试是相互独立的．记为该毕业生得到面试的公司个数，若P（＝0）＝．
（1）求p的值：
（2）求随机变量的分布列及数学期望．