高中数学随机思想的发展解答题

(本小题满分13分)
重庆电视台的一个智力游戏节目中，有一道将中国四大名著A、B、C、D与它们的作者
连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对
一个得3分，连错得分，一名观众随意连线，将他的得分记作ξ．
（Ⅰ）求该观众得分ξ为正数的概率；
（Ⅱ）求ξ的分布列及数学期望．

（本小题满分12分）
为了评估天气对大运会的影响，制定相应预案，深圳市气象局通过对最近50多年的气象数据资料的统计分析，发现8月份是我市雷电天气高峰期，在31天中平均发生雷电14.57天（如图7）．如果用频率作为概率的估计值，并假定每一天发生雷电的概率均相等，且相互独立．
（1）求在大运会开幕（8月12日）后的前3天比赛中，恰好有2天发生雷电天气的概率（精确到0.01）；
（2）设大运会期间（8月12日至23日，共12天），发生雷电天气的天数为，求的数学期望和方差．

（本小题满分12分）
某地区对12岁儿童瞬时记忆能力进行调查．瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人，下表为该班学生瞬时记忆能力的调查结果．例如表中听觉记忆能力为中等，且视觉记忆能力偏高的学生为3人．

视觉	视觉记忆能力
偏低	中等	偏高	超常
听觉 记忆 能力	偏低	0	7	5	1
中等	1	8	3
偏高	2		0	1
超常	0	2	1	1

由于部分数据丢失，只知道从这40位学生中随机抽取一个，视觉记忆能力恰为中等，且听觉记忆能力为中等或中等以上的概率为．
（1）试确定、的值；
（2）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
（3）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为，求随机变量的数学期望．

在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.以 $\xi$表示笼内还剩下的果蝇的只数.
（Ⅰ）写出 $\xi$的分布列（不要求写出计算过程）；
（Ⅱ）求数学期望 $E\xi$；
（Ⅲ）求概率 $P(\xi \ge E\xi )$.

投到某杂志的稿件，先由两位初审专家进行评审．若能通过两位初审专家的评审，则予以录用；若两位初审专家都未予通过，则不予录用；若恰能通过一位初审专家的评
审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录用．设稿件能通过各初审专家评审的概率均为 $0.5$，复审的稿件能通过评审的概率为 $0.3$．各专家独立评审．
（I）求投到该杂志的1篇稿件被录用的概率；
（II）记 $X$表示投到该杂志的4篇稿件中被录用的篇数，求 $X$的分布列及期望．

(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.
求：（I）打满3局比赛还未停止的概率；
（II）比赛停止时已打局数的分别列与期望E.

第16届亚运会将于2010年11月12日至27日在中国广州进行，在安全保障方面，警方从武警训练基地挑选防爆警察，从体能、射击、反应三项指标进行检测，如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士（分别记为A、B、C、D）拟参加挑选，且每人能通过体能、射击、反应的概率分别为。这三项测试能否通过相互之间没有影响。试卷
（1）求A能够入选的概率；试卷                                                                                                                                                                                                                                                                                                                                                                  
（2）规定：按人选人数得训练经费（每人选1人，则相应的训练基地得到3000元的训练经费），求该基地得到训练经费的分布列与数学期望。

某次有奖竞猜活动设有、两组相互独立的问题，答对问题可赢得奖金3000元，答对问题可赢得奖金6000元．规定答题顺序可任选，但只有一个问题答对后才能解答下一个问题，否则中止答题，假设你答对问题、的概率依次为．
（Ⅰ）若你按先后的次序答题，写出你获得奖金的数额的分布列及期望；
（Ⅱ）你认为获得奖金期望的大小与答题顺序有关吗？证明你的结论．

（本题12分）某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为为P₁，P₂，P₃，又知P₁，P₂是方程25x²－15x＋a＝0的两个根，且P₂＝P₃，
（1）求P₁，P₂，P₃的值；
（2）记表示销售两台这种家用电器的销售利润总和，求的分布列；
（3）求销售两台这种家用电器的销售利润总和的平均值。

（本小题满分12分）
某班级甲组有名学生，其中有名女生；乙组有名学生，其中有名女生.
（Ⅰ）若从两组中各抽取两人进行心理健康测试，求每组至少抽到一名女生的概率；
（Ⅱ）现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽
取名学生进行心理健康测试.
（）求从甲、乙两组各抽取的人数；
（）记表示抽取的名学生中男生人数，求的分布列及数学期望.

（本小题10分）口袋中有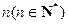个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若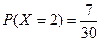，求：
（1）n的值；
（2）X的概率分布与数学期望．

(本小题满分12分)
某单位举办2010年上海世博会知识宣传活动，进行现场抽奖．盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖，否则，均为不获奖．卡片用后放回盒子，下一位参加者继续重复进行．
(Ⅰ)活动开始后，一位参加者问：盒中有几张“海宝”卡?主持人答：我只知道，从盒中抽取两张都是“世博会会徽”卡的概率是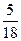，求抽奖者获奖的概率；
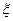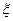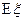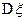(Ⅱ)现有甲乙丙丁四人依次抽奖，用表示获奖的人数，求的分布列及，的值．

为了更好地服务于2010年世博会，上海某酒店随机地对最近入住的名旅客进行服务质量问卷调查，把旅客对住宿的舒适满意度与价格满意度分为五个等级：
“1级（很不满意）”、“2级（不满意）”、“3级（一般）”、“4级（满意）”、“5级（很满意）”其结果如表所示，若在这个样本中，任选一人，其舒适度为，价格满意度.

(1)根据样本中的数据求P（y=5）及P（x≥3且y=3）的值；
(2)若的期望值为，求a、b、c的值；
(3)求该人在对价格满意（满意度不低于3）的条件下对舒适度也满意的概率.

上海世博会上有一种舞台灯，外形是正六棱柱，在其每个侧面（编号分别是①②③④⑤⑥）上安装5只颜色各异的灯，每只灯正常发光的概率是0.5，若一侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用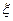表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个侧面面上恰有2个侧面需要更换的概率。
（3）写出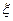的分布列，并求出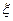的数学期望。

17．（本小题满分12分）
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示．
（1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（图4），再根据频率分布直方图估计这507个画师中年龄在岁的人数（结果取整数）；
（2）在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动，其中选取2名画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为ξ，求ξ的分布列及数学期望．

分组 （单位：岁）	频数	频率
	5	0.050
	①	0.200
	35	②
	30	0.300
	10	0.100
合计	100	1.00