投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录用.设稿件能通过各初审专家评审的概率均为
,复审的稿件能通过评审的概率为
.各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)记
表示投到该杂志的4篇稿件中被录用的篇数,求
的分布列及期望.
相关知识点
推荐套卷
 ; 2)
; 2)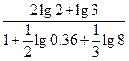
 的奇偶性和单调性(不要求给出证明);
的奇偶性和单调性(不要求给出证明); 的值域为
的值域为 ,求实数
,求实数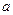 的取值范围
的取值范围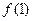 ;
; 在
在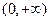 上是增函数;
上是增函数;
 的解析式;
的解析式;  (
(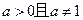 )在区间
)在区间 上减函数,求实数
上减函数,求实数 的取值范围?
的取值范围? 粤公网安备 44130202000953号
粤公网安备 44130202000953号