某超市在节日期间进行有奖促销，规定凡在该超市购物满400元的顾客，均可获得一次摸奖机会．摸奖规则如下：
奖盒中放有除颜色不同外其余完全相同的4个球（红、黄、黑、白）．顾客不放回的每次摸出1个球，若摸到黑球则摸奖停止，否则就继续摸球．按规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次摸奖停止的概率；
（2）记
为1名顾客摸奖获得的奖金数额，求随机变量的分布列和数学期望．
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).
（2）转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
（3）演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为
,求的分布列及数学期望
.
地为绿化环境，移栽了银杏树
棵，梧桐树
棵.它们移栽后的成活率分别
为
、
，每棵树是否存活互不影响，在移栽的
棵树中：
（1）求银杏树都成活且梧桐树成活棵的概率；
（2）求成活的棵树
的分布列与期望.
为推进成都市教育均衡发展，某中学需进一步壮大教师队伍，拟准备招聘一批优秀大学生到本单位就业，但在签约前要对他们的师范生素质进行测试。在待测试的某一个小组中有男、女生共10人（其中女生人数多于男生人数），如果从中随机选2人参加测试，其中恰为一男一女的概率为
。（1）求该小组中女生的人数；（2）假设此项专业技能测试对该小组的学生而言，每个女生通过的概率均为
，每个男生通过的概率均为
。现对该小组中男生甲．男生乙和女生丙3个人进行测试，记这3人中通过测试的人数为随机变量
，求的分布列和数学期望．
甲、乙、丙三位同学彼此独立地从A、B、C、D、E五所高校中，任选2所高校参加自主招生考试（并且只能选2所高校），但同学甲特别喜欢A高校，他除选A校外，在B、C、D、E中再随机选1所；同学乙和丙对5所高校没有偏爱，都在5所高校中随机选2所即可．
（1）求甲同学未选中E高校且乙、丙都选中E高校的概率；
（2）记X为甲、乙、丙三名同学中未参加E校自主招生考试的人数，求X的分布列及数学期望.
某煤矿发生透水事故时，作业区有若干人员被困．救援队从入口进入之后有
两条巷道通往作业区(如下图)，
巷道有
三个易堵塞点，各点被堵塞的概率都是
；
巷道有
两个易堵塞点，被堵塞的概率分别为
．
（1）求巷道中，三个易堵塞点最多有一个被堵塞的概率；
（2）若巷道中堵塞点个数为
，求的分布列及数学期望
，并按照＂平均堵塞点少的巷道是较好的抢险路线＂的标准，请你帮助救援队选择一条抢险路线，并说明理由．
某市教育局为了了解高三学生体育达标情况，在某学校的高三学生体育达标成绩中随机抽取100个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示：
若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：
（1）已知学生甲和学生乙的成绩均在第四组，求学生甲和学生乙至少有一人被选中复查的概率；
（2）在已抽取到的6名学生中随机抽取3名学生接受篮球项目的考核，设第三组中有三名学生接受篮球项目的考核，求暑的分布列和数学期望．
一批产品需要进行质量检验，质检部门规定的检验方案是：先从这批产品中任取3件作检验，若3件产品都是合格品，则通过检验；若有2件产品是合格品，则再从这批产品中任取1件作检验，这1件产品是合格品才能通过检验；若少于2件合格品，则不能通过检验，也不再抽检. 假设这批产品的合格率为80%，且各件产品是否为合格品相互独立.
(1)求这批产品通过检验的概率；
(2)已知每件产品检验费为125元，并且所抽取的产品都要检验，记这批产品的检验费为
元，求的概率分布及数学期望.
如图，一半径为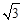
的圆形靶内有一个半径为
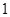的同心圆，将大圆分成两
部分，小圆内部区域记为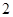
环，圆环区域记为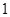环，某同学向该靶投掷
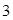枚飞镖，每次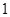枚. 假设他每次必
定会中靶，且投中靶内各点是随机的.
（1）求该同学在一次投掷中获得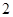环的概率；
（2）设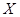
表示该同学在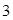次投掷中获得的环数，求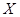的分布列及数学期望.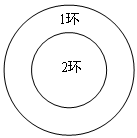
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖. 已知教师甲投进每个球的概率都是
．
（1）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；
（2）求教师甲在一场比赛中获奖的概率；
（3）已知教师乙在某场比赛中，6个球中恰好投进了4个球，求教师乙在这场比赛中获奖的概率；教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗？
某学校组织了一次安全知识竞赛，现随机抽取20名学生的测试成绩，如下表所示（不低于90分的测试成绩称为“优秀成绩”）：
| 79 |
90 |
82 |
80 |
84 |
95 |
79 |
86 |
89 |
91 |
| 97 |
86 |
79 |
78 |
86 |
77 |
87 |
89 |
83 |
85 |
（1）若从这20人中随机选取3人，求至多有1人是“优秀成绩”的概率；
（2）以这20人的样本数据来估计整个学校的总体数据，若从该校全体学生中（人数很多）任选3人，记
表示抽到“优秀成绩”学生的人数，求的分布列及数学期望.
为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3） 现从A班的上述5名学生中随机选取3名学生，用X表示其中视力大于4.6的人数，求X的分布列和数学期望.
某商场举行的"三色球"购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：
| 奖级 |
摸出红、蓝球个数 |
获奖金额 |
| 一等奖 |
3红1蓝 |
200元 |
| 二等奖 |
3红0蓝 |
50元 |
| 三等奖 |
2红1蓝 |
10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级．
（1）求一次摸奖恰好摸到1个红球的概率；
（2）求摸奖者在一次摸奖中获奖金额的分布列与期望
．
(14分)某工厂在试验阶段大量生产一种零件，这种零件有
、
两项技术指标需要检测，设各项技术指标达标与否互不影响.若仅有A项技术指标达标的概率为
，A、B两项技术指标都不达标的概率为
．按质量检验规定：两项技术指标都达标的零件为合格品．
（1）求一个零件经过检测为合格品的概率？
（2）若任意抽取该种零件4个，设
表示其中合格品的个数，求的分布列及数学期望
．
假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为
，记此时教室里敞开的窗户个数为X．
(1)求X的分布及数学期望；
(2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．
粤公网安备 44130202000953号
