高中数学随机思想的发展填空题

某市有一个玉米种植基地．该基地的技术员通过种植实验发现，一种品质优良的玉米种子每粒发芽的概率都为0.95，现在该种植基地播种了10000粒这种玉米种子，对于没有发芽的种子，每粒需再播种1粒，补种的种子数记为，则的数学期望 .

某市有一个玉米种植基地．该基地的技术员通过种植实验发现，一种品质优良的玉米种子每粒发芽的概率都为0.95，现在该种植基地播种了10000粒这种玉米种子，对于没有发芽的种子，每粒需再播种1粒，补种的种子数记为，则的数学期望 .

已知随机变量X的方差V（X）=1，设随机变量Y=2X+3，则V（Y）= ．

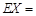（本小题满分12分）某校学生会进行了一次关于“消防安全”的调查活动，组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查．活动结束后，团委会对问卷结果进行了统计，并将其中“是否知道灭火器使用方法（知道或不知道）”的调查结果统计如下表：

年龄（岁）	[10,20）	[20,30）	[30,40）	[40,50）	[50,60）	[60,70]
频数	m	n	15	10	7	3
知道的人数	4	6	12	6	3	2

表中所调查的居民年龄在[10,20），[20,30），[30,40）的人数成等差数列．
（Ⅰ）求上表中的m，n值，若从年龄在[20,30）的居民中随机选取两人，求这两人至少有一人知道灭火器使用方法的概率；
（Ⅱ）在被调查的居民中，若从年龄在[10,20），[20,30）的居民中各随机选取2人参加消防知识讲座，记选中的4人中不知道灭火器使用方法的人数为，求随机变量的分布列和数学期望．

为了分析某篮球运动员在比赛中发挥的稳定程度，统计了该运动员在6场比赛中的得分，用茎叶图表示如图，则该组数据的方差为.

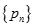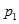随机变量X的分布列如下表所示，若数列是以为首项，以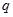为公比的等比数列，则称随机变量X服从等比分布，记为Q(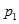,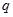)．现随机变量X～Q(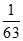,2)．

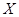	1	2	…	n
			…

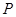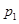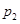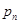（1）求n 的值并求随机变量X的数学期望EX；
（2）一个盒子里装有标号为1，2，…，n且质地相同的标签若干张，从中任取1张标签所得的标号为随机变量X．现有放回的从中每次抽取一张，共抽取三次，求恰好2次取得标签的标号不大于3的概率．

袋中有大小、质地均相同的4个红球与2个白球．若从中有放回地依次取出一个球，记6次取球中取出红球的次数为ξ，则ξ的期望E(ξ)＝________.

随机变量ξ的分布列如下

ξ	－1	0	1
P	a	b	c

其中a，b，c成等差数列，若E(ξ)＝，则D(ξ)＝________.

某学生在参加政、史、地三门课程的学业水平考试中，取得A等级的概率分别为、、，且三门课程的成绩是否取得A等级相互独立．记ξ为该生取得A等级的课程数，其分布列如表所示，则数学期望E(ξ)的值为________．

ξ	0	1	2	3
P		a	b

某游戏的得分为1,2,3,4,5，随机变量 $\xi$表示小白玩游戏的得分.若 $E\left(\xi \right)$=4.2，则小白得5分的概率至少为.

设随机变量,则.

某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为 $\frac{2}{3}$，得到乙、丙公司面试的概率均为 $P$，且三个公司是否让其面试是相互独立的．记 $X$为该毕业生得到面试的公司个数．若 $P(X=0)=\frac{1}{12}$，则随机变量 $X$的数学期望 $E\left(X\right)=$．

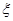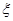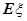小李练习射击，每次击中目标的概率为，用表示小李射击次击中目标的次数，则的均值与方差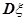的值分别是______________________．

如图，将一个各面都涂了油漆的正方体，切割成125个同样大小的小正方体．经过搅拌后，从中随机取出一个小正方体，记它的涂油漆面数为X，则X的均值为E(X)＝________．

设随机变量的概率分布律如下表所示：

其中，，成等差数列，若随机变量的的均值为，则的方差为___________．