某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为 ,求
,求 的分布列及数学期望
的分布列及数学期望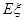 .
.
相关知识点
推荐套卷
 的部分图象如图所示.
的部分图象如图所示. 的解析式,并写出
的解析式,并写出 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且 的值.
的值.
 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队. 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段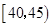 中的概率;
中的概率;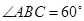 ,平面
,平面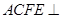 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a. 平面ACFE;
平面ACFE;
 的首项
的首项 ,公差
,公差 ,等比数列
,等比数列 满足
满足
 对任意
对任意 均有
均有 ,求数列
,求数列 .
. 的部分图象如图所示.
的部分图象如图所示. 的解析式,并写出
的解析式,并写出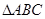 的内角分别是A,B,C,若
的内角分别是A,B,C,若 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号