山东省淄博市高三复习阶段性诊断考试理科数学试卷
设 是两个非零向量,则下列命题为真命题的是
是两个非零向量,则下列命题为真命题的是
|
A.若

C.若
 ,则存在实数
,则存在实数 ,使得
,使得
D.若存在实数
 ,使得
,使得 ,则
,则
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是
A. |
B.6 | C.4 | D. |
3名男生3名女生站成两排照相,要求每排3人且3名男生不在同一排,则不同的站法有
| A.324种 | B.360种 | C.648种 | D.684种 |
如图,已知双曲线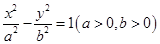 的左、右焦点分别为
的左、右焦点分别为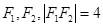 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点, 轴交于点A,
轴交于点A,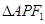 的内切圆在
的内切圆在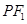 上的切点为Q,若
上的切点为Q,若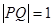 ,则双曲线的离心率是
,则双曲线的离心率是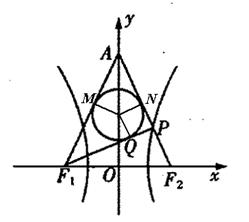
| A.3 | B.2 | C.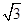 |
D.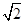 |
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 当且仅当“
当且仅当“ ”或“
”或“ ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若 ;
;
②若 ,则
,则 ;
;
③若 ,则对于任意
,则对于任意 ;
;
④对于任意向量 .
.
其中真命题的序号为__________.
某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
| 79 |
90 |
82 |
80 |
84 |
95 |
79 |
86 |
89 |
91 |
| 97 |
86 |
79 |
78 |
86 |
77 |
87 |
89 |
83 |
85 |
(1)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记 表示抽到“优秀成绩”学生的人数,求
表示抽到“优秀成绩”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
如图,在四棱锥P-ABCD中, 平面ABCD,AD//BC,
平面ABCD,AD//BC, AC,
AC,
 ,点M在线段PD上.
,点M在线段PD上.
(1)求证: 平面PAC;
平面PAC;
(2)若二面角M-AC-D的大小为 ,试确定点M的位置.
,试确定点M的位置.
某市为控制大气PM2.5的浓度,环境部门规定:该市每年的大气主要污染物排放总量不能超过55万吨,否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨,通过技术改造和倡导绿色低碳生活等措施,此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时,因为经济发展和人口增加等因素,每年又新增加大气主要污染物排放量 万吨.
万吨.
(1)从2014年起,该市每年大气主要污染物排放总量(万吨)依次构成数列 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;
(2)证明:数列 是等比数列;
是等比数列;
(3)若该市始终不需要采取紧急限排措施,求m的取值范围.
已知中心在原点,对称轴为坐标轴的椭圆C的一个焦点在抛物线 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
.
(1)求椭圆C的方程;
(2)点A为椭圆C的右顶点,过点 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.
 为
为



 等于
等于



 ”成立的
”成立的




 上单调递增的是
上单调递增的是



 展开式中,x的幂指数是整数的项共有
展开式中,x的幂指数是整数的项共有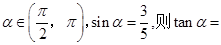 ________.
________. ________.
________. 的最小值为_________.
的最小值为_________. 的取值范围是________.
的取值范围是________. 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若 .
. ,求函数
,求函数 上的取值范围.
上的取值范围.
 的最大值;
的最大值; ,求
,求 的取值范围.
的取值范围. +
+
 (n
(n )
) 粤公网安备 44130202000953号
粤公网安备 44130202000953号