在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集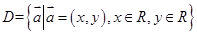 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量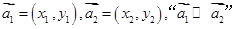 当且仅当“
当且仅当“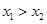 ”或“
”或“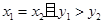 ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若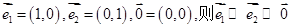 ;
;
②若 ,则
,则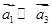 ;
;
③若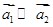 ,则对于任意
,则对于任意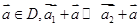 ;
;
④对于任意向量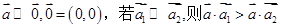 .
.
其中真命题的序号为__________.
推荐套卷
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集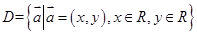 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量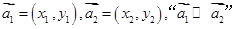 当且仅当“
当且仅当“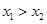 ”或“
”或“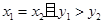 ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若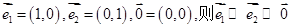 ;
;
②若 ,则
,则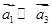 ;
;
③若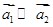 ,则对于任意
,则对于任意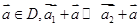 ;
;
④对于任意向量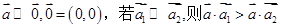 .
.
其中真命题的序号为__________.