如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=AF=1.
(1)求四棱锥F﹣ABCD的体积VF﹣ABCD;
(2)求证:平面AFC⊥平面CBF;
(3)在线段CF上是否存在一点M,使得OM∥平面ADF,并说明理由.
如图,三棱柱 的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.
的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.

(1)求证:B1C//平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
如图所示,已知空间四边形 的每条边和对角线长都等于1,点
的每条边和对角线长都等于1,点 ,
, ,
, 分别是
分别是 、
、 、
、 的中点,计算:
的中点,计算:
(1) ;
;
(2) 的长;
的长;
(3)异面直线 与
与 所成角的余弦值.
所成角的余弦值.
如图,四棱锥 ,平面
,平面 ⊥平面
⊥平面 ,△
,△ 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且 .
.
(1)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)试问点 在线段
在线段 上什么位置时,二面角
上什么位置时,二面角 的大小为
的大小为 .
.
如图,已知正方形 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, 是线段
是线段 的中点.用向量方法证明与解答:
的中点.用向量方法证明与解答:

(1)求证: ∥平面
∥平面 ;
;
(2)试判断在线段 上是否存在一点
上是否存在一点 ,使得直线
,使得直线 与
与 所成角为
所成角为 ,并说明理由.
,并说明理由.
如图(1)示,在梯形 中,
中, ,
, ,且
,且 ,如图(2)沿
,如图(2)沿 将四边形
将四边形 折起,使得平面
折起,使得平面 与平面
与平面 垂直,
垂直, 为
为 的中点.
的中点.
(Ⅰ)求证:
(Ⅱ)求证: ;
;
(Ⅲ)求点D到平面BCE的距离。
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点.
的中点.
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)设点 是线段
是线段 上的一点,
上的一点, ,且
,且 平面
平面 .
.
(1)求实数 的值;
的值;
(2)若 ,且平面
,且平面 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
如图,在正方体 的棱长为
的棱长为 ,
, 为棱
为棱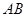 上的一动点.
上的一动点.

(1)若 为棱
为棱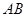 的中点,
的中点,
①求四棱锥 的体积
的体积
②求证:面 面
面
(2)若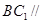 面
面 ,求证:
,求证: 为棱
为棱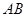 的中点.
的中点.