如图,已知正方形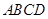 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直,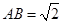 ,
,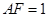 ,
,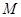 是线段
是线段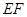 的中点.用向量方法证明与解答:
的中点.用向量方法证明与解答:
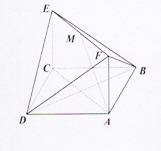
(1)求证: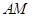 ∥平面
∥平面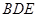 ;
;
(2)试判断在线段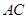 上是否存在一点
上是否存在一点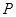 ,使得直线
,使得直线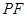 与
与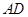 所成角为
所成角为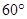 ,并说明理由.
,并说明理由.
相关知识点
推荐套卷
如图,已知正方形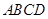 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直,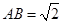 ,
,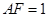 ,
,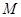 是线段
是线段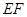 的中点.用向量方法证明与解答:
的中点.用向量方法证明与解答:

(1)求证: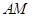 ∥平面
∥平面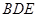 ;
;
(2)试判断在线段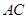 上是否存在一点
上是否存在一点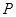 ,使得直线
,使得直线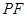 与
与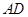 所成角为
所成角为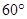 ,并说明理由.
,并说明理由.