如图,直三棱柱ABC﹣A′B′C′,∠BAC=90°, ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
(Ⅰ)证明:MN∥平面A′ACC′;
(Ⅱ)求三棱锥A′﹣MNC的体积.
(椎体体积公式V= Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
若直线l不平行于平面α,且l⊄α,则( )
| A.α内的所有直线与l异面 | B.α内不存在与l平行的直线 |
| C.α内存在唯一的直线与l平行 | D.α内的直线与l都相交 |
如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.
下列说法中:
①两条直线都和同一个平面平行,则这两条直线平行;
②在平行投影下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小完全相同;
③一个圆绕其任意一条直径旋转180°所形成的旋转体叫做球;
④a∥b,b⊂α⇒a∥α;
⑤已知三条两两异面的直线,则存在无穷多条直线与它们都相交.
则正确的序号是 .
一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:①AB⊥EF;②AB与CM成60°角;③EF与MN是异面直线;④MN∥CD,其中正确的是( )
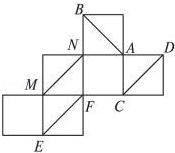
| A.①② | B.③④ | C.②③ | D.①③ |
已知直线a和两个平面α,β,给出下列四个命题:①若a∥α,则α内的任何直线都与a平行;②若a⊥α,则α内的任何直线都与a垂直;③若α∥β,则β内的任何直线都与α平行;④若α⊥β,则β内的任何直线都与α垂直.则其中( )
| A.②、③为真 | B.①、②为真 |
| C.①、③为真 | D.③、④为真 |
设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A.若m∥α,n∥α,则m∥n |
| B.若m∥α,m∥β,则α∥β |
| C.若m∥n,m⊥α,则n⊥α |
| D.若m∥α,α⊥β,则m⊥β |
对于不重合的两平面 ,给定下列条件:
,给定下列条件:
①存在平面 ,使得
,使得 都垂直于
都垂直于 ;
;
②存在平面 ,使得
,使得 都平行于
都平行于 ;
;
③存在直线 ;
;
④存在异面直线
其中可以判定 平行的条件有( )
平行的条件有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设 表示不同的直线,
表示不同的直线, 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题:
①若 ,且
,且 ,则
,则 ;
;
②若 ,且
,且 ,则
,则 ;
;
③若 ,
, ,
, ,则
,则 ;
;
④若 ,
, ,
, 且
且 ,则
,则 .
.
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |