高中数学误差估计解答题

从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：

质量指标 值分组	[75，85）	[85，95）	[95，105）	[105，115）	[115，125）
频数	6	26	38	22	8

 
（Ⅰ）在答题卡上列出这些数据频率分布表，并作出频率分布直方图；
（Ⅱ）估计这种产品质量指标值的平均值及方差（同一组中的数据用该组区间的中点值作代表）．

（本小题满分12分）某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图．
为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．
（1）求在这10个卖场中，甲型号电视机的“星级卖场”的个数；
（2）若在这10个卖场中，乙型号电视机销售量的平均数为26．7，求的概率；
（3）若a=1，记乙型号电视机销售量的方差为，根据茎叶图推断b为何值时，达到最小值．（只需写出结论）

某良种培育基地正在培育一种小麦新品种A，种植了25亩，所得亩产数据（单位：千克）如下：
363，371，374，383，385，386，391，392，394，394，395，397，397，400，401，401，403，406，407，410，412，415，416，422，430．
（1）求这二十五个数据的中位数；
（2）以组距为10进行分组，完成答题卡上的品种A亩产量的频率分布表；

分组	频数	频率
[420，430]
合计

 
完成答题卡上的品种A亩产量的频率分布直方图．

某班100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60），[60,70），[70,80），[80,90），[90,100]．
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；

（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如下表所示，求数学成绩在[50,90）之外的人数．

分数段	[50,60）	[60,70）	[70,80）	[80,90）
x∶y	1∶1	2∶1	3∶4	4∶5

 

（本小题满分10分）某校100位学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：、、、、．

（Ⅰ）求图中的值;
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分．

（本小题满分12分）
如图所示的茎叶图记录了甲、乙两个小组（每小组4人）在期末考试中的数学成绩．乙组记录中有一个数据模糊，无法确认，在图中以表示．已知甲、乙两个小组的数学成绩的平均分相同．

（1）求的值；
（2）求甲、乙两个小组数学成绩的方差,并说明哪个小组的成绩相对比较稳定；
参考公式： 

医生的专业能力参数可有效衡量医生的综合能力，越大，综合能力越强，并规定: 能力参数不少于30称为合格，不少于50称为优秀．某市卫生管理部门随机抽取300名医生进行专业能力参数考核，得到如图所示的能力的频率分布直方图:

（Ⅰ）求出这个样本的合格率、优秀率；
（Ⅱ）现用分层抽样的方法从中抽出一个样本容量为20的样本，再从这20名医生中随机选出2名．
①求这2名医生的能力参数为同一组的概率；
②设这2名医生中能力参数为优秀的人数为，求随机变量的分布列和期望．

（本大题满分12分）从某学校的名男生中随机抽取名测量身高，被测学生身高全部介于和之间，将测量结果按如下方式分成八组：第一组，第二组，第八组，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为人．

（Ⅰ）求第七组的频率；
（Ⅱ）估计该校的名男生的身高的中位数以及身高在以上（含）的人数；
（Ⅲ）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为，事件，事件，求

某班50名学生在一次数学测试中，成绩全部介于50与100之间，将测试结果按如下方式分成五组：第一组[50，60），第二组[60，70），…，第五组[90，100]．如图所示是按上述分组方法得到的频率分布直方图．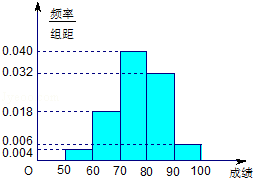

（Ⅰ）若成绩大于或等于60且小于80，认为合格，求该班在这次数学测试中成绩合格的人数；
（Ⅱ）从测试成绩在[50，60）∪[90，100]内的所有学生中随机抽取两名同学，设其测试成绩分别为m、n，求事件“|m﹣n|＞10”概率．

我校高三年级进行了一次水平测试．用系统抽样的方法抽取了50名学生的数学成绩，准备进行分析和研究．经统计成绩的分组及各组的频数如下：

[40，50）， 2；   [50，60）， 3；  [60，70）， 10；  [70，80）， 15；   [80，90）， 12；  [90，100]， 8．
（Ⅰ）完成样本的频率分布表；画出频率分布直方图．
（Ⅱ）估计成绩在85分以下的学生比例；
（Ⅲ）请你根据以上信息去估计样本的众数、中位数、平均数．（精确到0．01）

分组	频数	频率
[40，50）	2
[50，60）	3
[60，70）	10
[70，80）	15
[80，90）	12
[90，100]	8
合计	50

 

（本小题满分13分）某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，整理得到数据分组及频率分布表和频率分布直方图： 

分组（日销售量）	频率（甲种酸奶）
[ 0，10]	0．10
（10，20]	0．20
（20，30]	0．30
（30，40]	0．25
（40，50]	0．15

 

（Ⅰ）写出频率分布直方图中的的值，并作出甲种酸奶日销售量的频率分布直方图；

（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为，，试比较与的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月（按30天计算）的销售总量．

（本小题满分12分）在科普知识竞赛前的培训活动中，将甲、乙两名学生的6次培训成绩（百分制）制成如图所示的茎叶图：
   
（Ⅰ）若从甲、乙两名学生中选择1人参加该知识竞赛，你会选哪位？请运用统计学的知识说明理由；
（Ⅱ）若从学生甲的6次培训成绩中随机选择2个，记选到的分数超过87分的个数为，求的分布列和数学期望．

在一次考试中，5名同学数学、物理成绩如下表所示：

学生	A	B	C	D	E
数学（x分）	89	91	93	95	97
物理（y分）	87	89	89	92	93

 
（1）根据表中数据，求物理分对数学分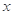的回归方程：
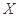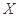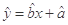（2）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以表示选中的同学中物理成绩高于90分的人数，求随机变量的分布列及数学期望．（附：回归方程中，，）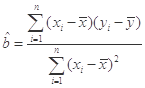

（本小题满分12分）某中学在高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名.为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核.
（1）求抽取的5人中男、女同学的人数；
（2）考核前，评估小组打算从抽取的5人中随机选出2名同学进行访谈，求选出的两名同学中恰有一名女同学的概率.

（本小题满分12分）根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在为优秀，人类可正常活动．某市环保局对该市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为，， ， ，由此得到样本的空气质量指数频率分布直方图．

（Ⅰ）若空气质量指数大于或等于15且小于35认为是良好的，求该市在这次监测中空气质量
为良好的天数，并根据频率分布直方图估计这一年度的空气质量指数的平均值；
（Ⅱ）如果空气质量指数不超过15，就认定空气质量为“优”，则从这一年的监测数据中随机
抽取3天的数值，其中达到“优”的天数为，求的分布列和数学期望．