(本小题满分12分)某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求 的概率;
的概率;
(3)若a=1,记乙型号电视机销售量的方差为 ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时, 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
相关知识点
推荐套卷
 ,
, ,
, .
. 与
与 的大小;
的大小; .
.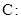
 (
( )的上顶点为
)的上顶点为 ,
, 是
是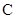 上的一点,以
上的一点,以 为直径的圆经过椭圆
为直径的圆经过椭圆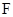 .
.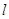 与椭圆
与椭圆 轴上是否存在两个定点,它们到直线
轴上是否存在两个定点,它们到直线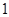 ?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
?如果存在,求出这两个定点的坐标;如果不存在,说明理由.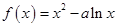 在
在 是增函数,
是增函数, 在
在 为减函数.
为减函数. ,
,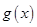 的表达式;
的表达式; 时,方程
时,方程 有唯一解;
有唯一解; 时,若
时,若 在
在 内恒成立,求
内恒成立,求 的取值范围.
的取值范围.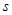 万件与促销费用
万件与促销费用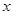 万元满足
万元满足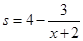 .已知
.已知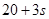 万元,商品的销售价格定为
万元,商品的销售价格定为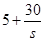 元/件.
元/件.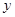 万元表示为促销费用
万元表示为促销费用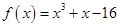 .
.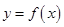 在点
在点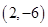 处的切线方程;
处的切线方程; 为曲线
为曲线 粤公网安备 44130202000953号
粤公网安备 44130202000953号